Longquan Dai
Hardware-Efficient Guided Image Filtering For Multi-Label Problem
Feb 28, 2018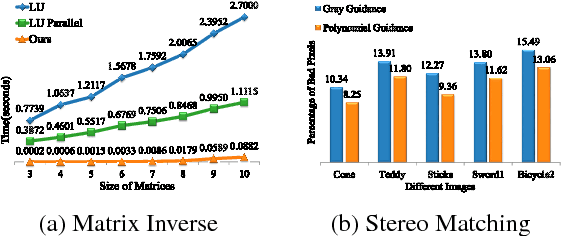


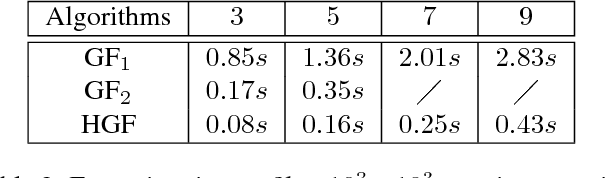
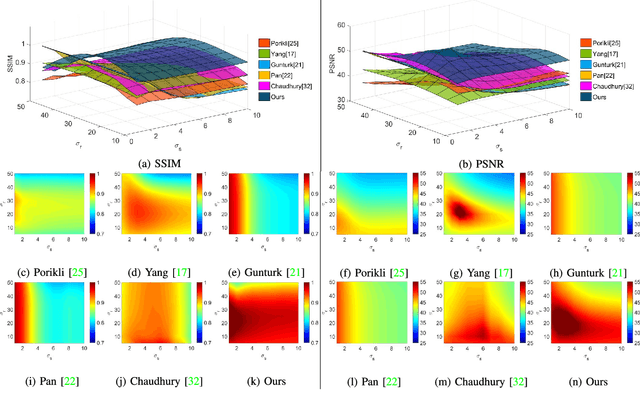
Abstract:The Guided Filter (GF) is well-known for its linear complexity. However, when filtering an image with an n-channel guidance, GF needs to invert an n x n matrix for each pixel. To the best of our knowledge existing matrix inverse algorithms are inefficient on current hardwares. This shortcoming limits applications of multichannel guidance in computation intensive system such as multi-label system. We need a new GF-like filter that can perform fast multichannel image guided filtering. Since the optimal linear complexity of GF cannot be minimized further, the only way thus is to bring all potentialities of current parallel computing hardwares into full play. In this paper we propose a hardware-efficient Guided Filter (HGF), which solves the efficiency problem of multichannel guided image filtering and yields competent results when applying it to multi-label problems with synthesized polynomial multichannel guidance. Specifically, in order to boost the filtering performance, HGF takes a new matrix inverse algorithm which only involves two hardware-efficient operations: element-wise arithmetic calculations and box filtering. In order to break the linear model restriction, HGF synthesizes a polynomial multichannel guidance to introduce nonlinearity. Benefiting from our polynomial guidance and hardware-efficient matrix inverse algorithm, HGF not only is more sensitive to the underlying structure of guidance but also achieves the fastest computing speed. Due to these merits, HGF obtains state-of-the-art results in terms of accuracy and efficiency in the computation intensive multi-label
Speeding Up the Bilateral Filter: A Joint Acceleration Way
Feb 28, 2018
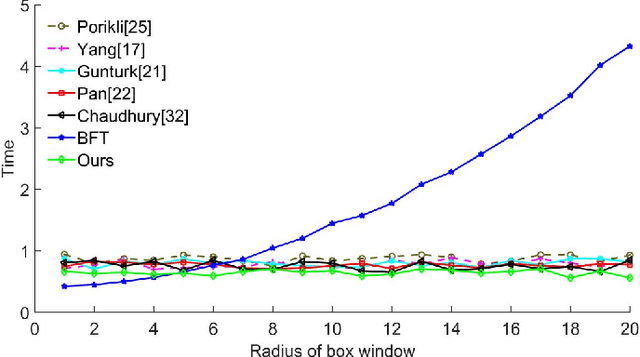
Abstract:Computational complexity of the brute-force implementation of the bilateral filter (BF) depends on its filter kernel size. To achieve the constant-time BF whose complexity is irrelevant to the kernel size, many techniques have been proposed, such as 2D box filtering, dimension promotion, and shiftability property. Although each of the above techniques suffers from accuracy and efficiency problems, previous algorithm designers were used to take only one of them to assemble fast implementations due to the hardness of combining them together. Hence, no joint exploitation of these techniques has been proposed to construct a new cutting edge implementation that solves these problems. Jointly employing five techniques: kernel truncation, best N -term approximation as well as previous 2D box filtering, dimension promotion, and shiftability property, we propose a unified framework to transform BF with arbitrary spatial and range kernels into a set of 3D box filters that can be computed in linear time. To the best of our knowledge, our algorithm is the first method that can integrate all these acceleration techniques and, therefore, can draw upon one another's strong point to overcome deficiencies. The strength of our method has been corroborated by several carefully designed experiments. In particular, the filtering accuracy is significantly improved without sacrificing the efficiency at running time.
Interpreting and Extending The Guided Filter Via Cyclic Coordinate Descent
May 30, 2017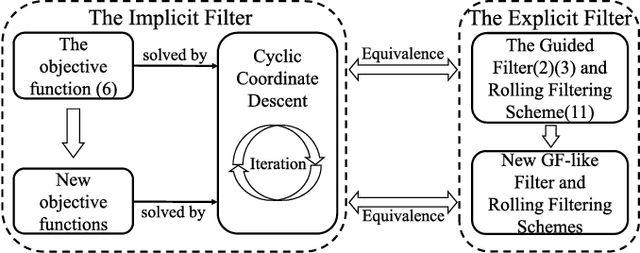

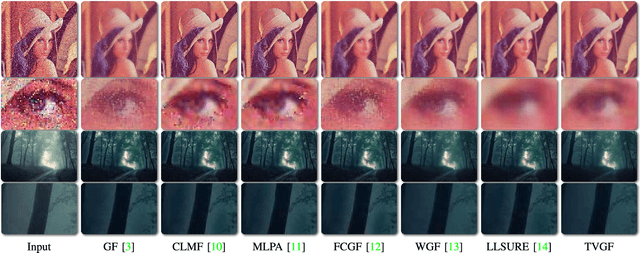
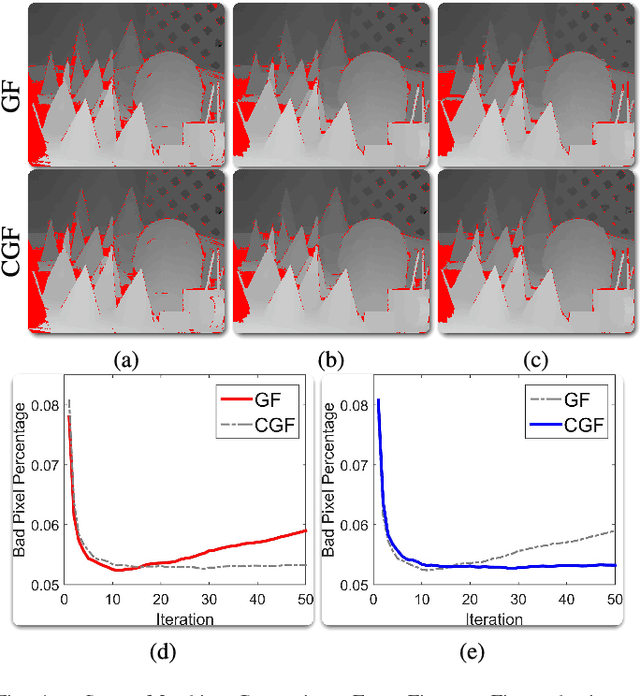
Abstract:In this paper, we will disclose that the Guided Filter (GF) can be interpreted as the Cyclic Coordinate Descent (CCD) solver of a Least Square (LS) objective function. This discovery implies a possible way to extend GF because we can alter the objective function of GF and define new filters as the first pass iteration of the CCD solver of modified objective functions. Moreover, referring to the iterative minimizing procedure of CCD, we can derive new rolling filtering schemes. Hence, under the guidance of this discovery, we not only propose new GF-like filters adapting to the specific requirements of applications but also offer thoroughly explanations for two rolling filtering schemes of GF as well as the way to extend them. Experiments show that our new filters and extensions produce state-of-the-art results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge