Interpreting and Extending The Guided Filter Via Cyclic Coordinate Descent
Paper and Code
May 30, 2017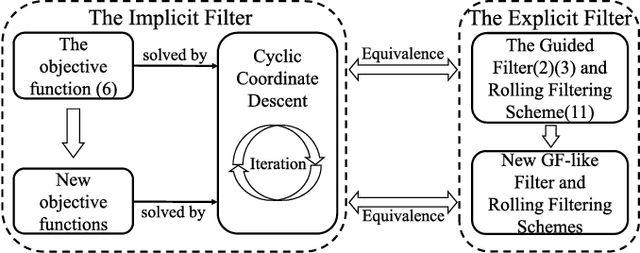

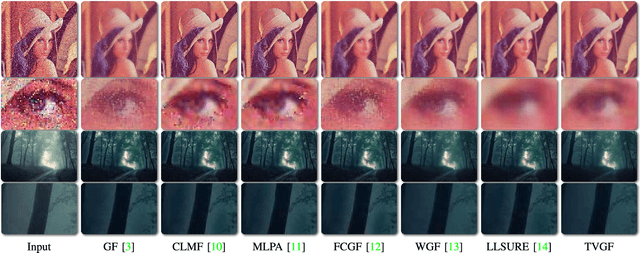
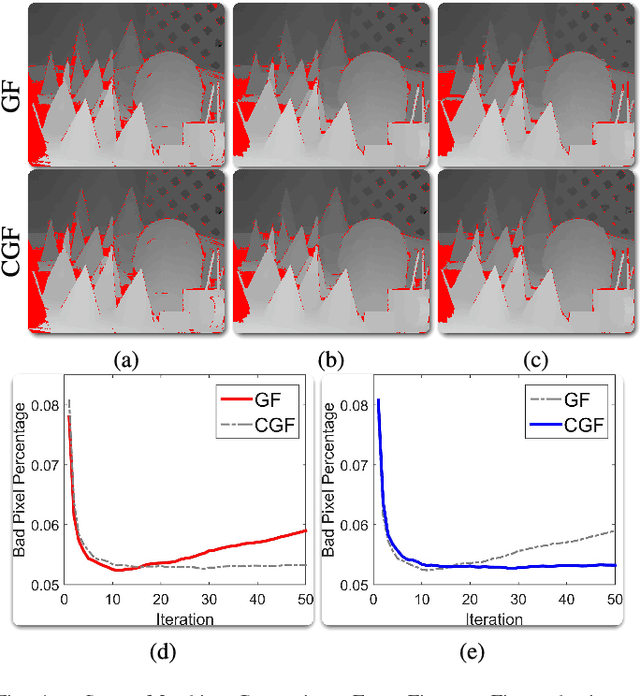
In this paper, we will disclose that the Guided Filter (GF) can be interpreted as the Cyclic Coordinate Descent (CCD) solver of a Least Square (LS) objective function. This discovery implies a possible way to extend GF because we can alter the objective function of GF and define new filters as the first pass iteration of the CCD solver of modified objective functions. Moreover, referring to the iterative minimizing procedure of CCD, we can derive new rolling filtering schemes. Hence, under the guidance of this discovery, we not only propose new GF-like filters adapting to the specific requirements of applications but also offer thoroughly explanations for two rolling filtering schemes of GF as well as the way to extend them. Experiments show that our new filters and extensions produce state-of-the-art results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge