Speeding Up the Bilateral Filter: A Joint Acceleration Way
Paper and Code
Feb 28, 2018
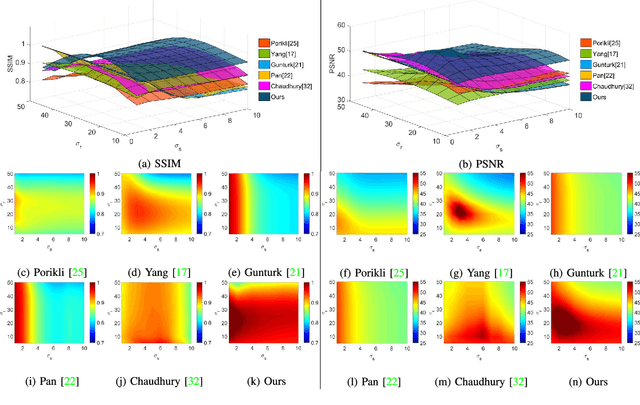
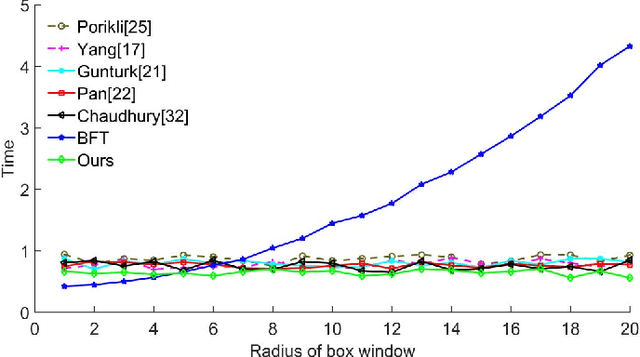
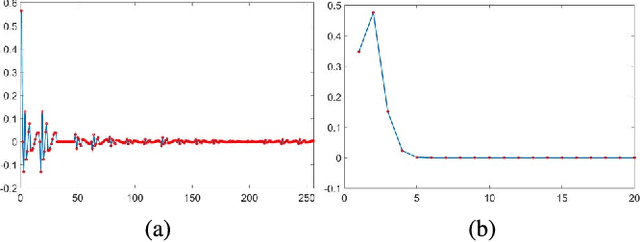
Computational complexity of the brute-force implementation of the bilateral filter (BF) depends on its filter kernel size. To achieve the constant-time BF whose complexity is irrelevant to the kernel size, many techniques have been proposed, such as 2D box filtering, dimension promotion, and shiftability property. Although each of the above techniques suffers from accuracy and efficiency problems, previous algorithm designers were used to take only one of them to assemble fast implementations due to the hardness of combining them together. Hence, no joint exploitation of these techniques has been proposed to construct a new cutting edge implementation that solves these problems. Jointly employing five techniques: kernel truncation, best N -term approximation as well as previous 2D box filtering, dimension promotion, and shiftability property, we propose a unified framework to transform BF with arbitrary spatial and range kernels into a set of 3D box filters that can be computed in linear time. To the best of our knowledge, our algorithm is the first method that can integrate all these acceleration techniques and, therefore, can draw upon one another's strong point to overcome deficiencies. The strength of our method has been corroborated by several carefully designed experiments. In particular, the filtering accuracy is significantly improved without sacrificing the efficiency at running time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge