Quantifying and Learning Disentangled Representations with Limited Supervision

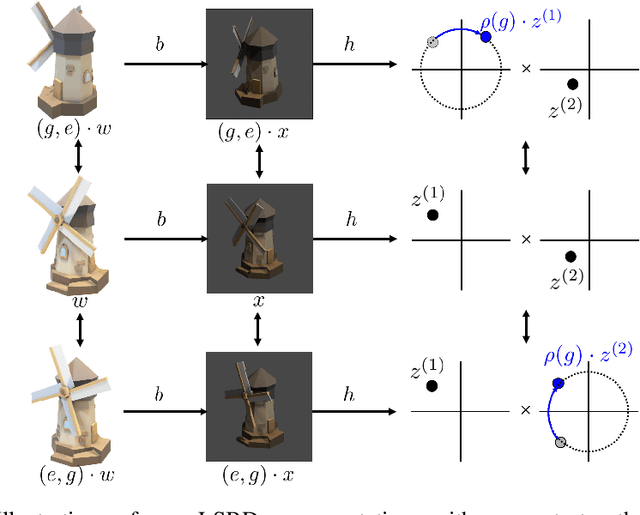
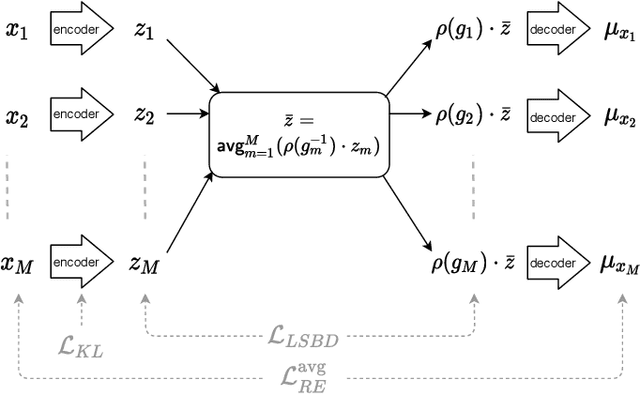
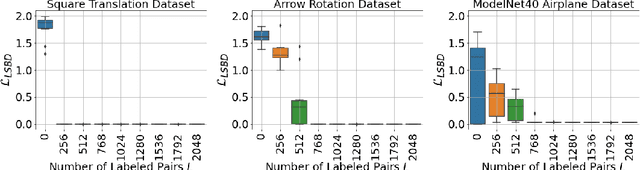
Learning low-dimensional representations that disentangle the underlying factors of variation in data has been posited as an important step towards interpretable machine learning with good generalization. To address the fact that there is no consensus on what disentanglement entails, Higgins et al. (2018) propose a formal definition for Linear Symmetry-Based Disentanglement, or LSBD, arguing that underlying real-world transformations give exploitable structure to data. Although several works focus on learning LSBD representations, such methods require supervision on the underlying transformations for the entire dataset, and cannot deal with unlabeled data. Moreover, none of these works provide a metric to quantify LSBD. We propose a metric to quantify LSBD representations that is easy to compute under certain well-defined assumptions. Furthermore, we present a method that can leverage unlabeled data, such that LSBD representations can be learned with limited supervision on transformations. Using our LSBD metric, our results show that limited supervision is indeed sufficient to learn LSBD representations.

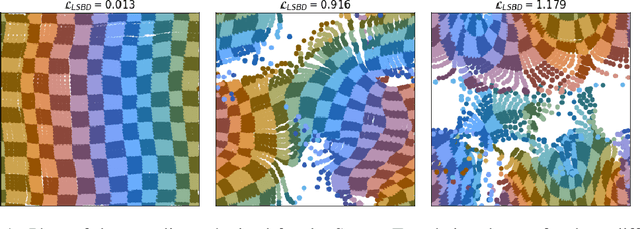
A Metric for Linear Symmetry-Based Disentanglement

The definition of Linear Symmetry-Based Disentanglement (LSBD) proposed by (Higgins et al., 2018) outlines the properties that should characterize a disentangled representation that captures the symmetries of data. However, it is not clear how to measure the degree to which a data representation fulfills these properties. We propose a metric for the evaluation of the level of LSBD that a data representation achieves. We provide a practical method to evaluate this metric and use it to evaluate the disentanglement of the data representations obtained for three datasets with underlying $SO(2)$ symmetries.

Anomaly Detection for imbalanced datasets with Deep Generative Models

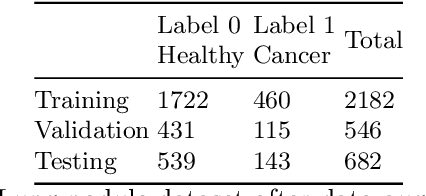
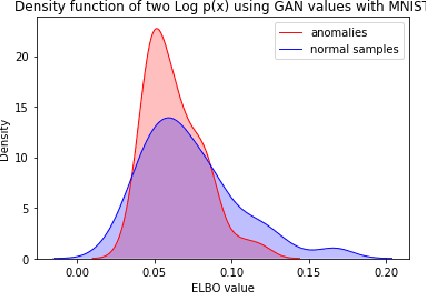
Many important data analysis applications present with severely imbalanced datasets with respect to the target variable. A typical example is medical image analysis, where positive samples are scarce, while performance is commonly estimated against the correct detection of these positive examples. We approach this challenge by formulating the problem as anomaly detection with generative models. We train a generative model without supervision on the `negative' (common) datapoints and use this model to estimate the likelihood of unseen data. A successful model allows us to detect the `positive' case as low likelihood datapoints. In this position paper, we present the use of state-of-the-art deep generative models (GAN and VAE) for the estimation of a likelihood of the data. Our results show that on the one hand both GANs and VAEs are able to separate the `positive' and `negative' samples in the MNIST case. On the other hand, for the NLST case, neither GANs nor VAEs were able to capture the complexity of the data and discriminate anomalies at the level that this task requires. These results show that even though there are a number of successes presented in the literature for using generative models in similar applications, there remain further challenges for broad successful implementation.