Quantifying and Learning Disentangled Representations with Limited Supervision

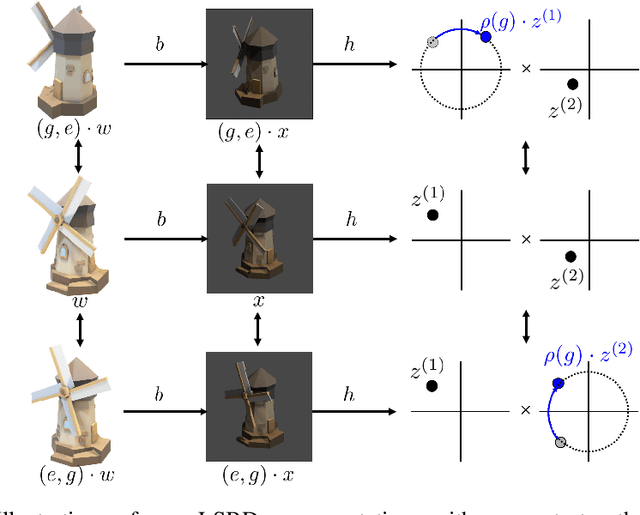
Learning low-dimensional representations that disentangle the underlying factors of variation in data has been posited as an important step towards interpretable machine learning with good generalization. To address the fact that there is no consensus on what disentanglement entails, Higgins et al. (2018) propose a formal definition for Linear Symmetry-Based Disentanglement, or LSBD, arguing that underlying real-world transformations give exploitable structure to data. Although several works focus on learning LSBD representations, such methods require supervision on the underlying transformations for the entire dataset, and cannot deal with unlabeled data. Moreover, none of these works provide a metric to quantify LSBD. We propose a metric to quantify LSBD representations that is easy to compute under certain well-defined assumptions. Furthermore, we present a method that can leverage unlabeled data, such that LSBD representations can be learned with limited supervision on transformations. Using our LSBD metric, our results show that limited supervision is indeed sufficient to learn LSBD representations.

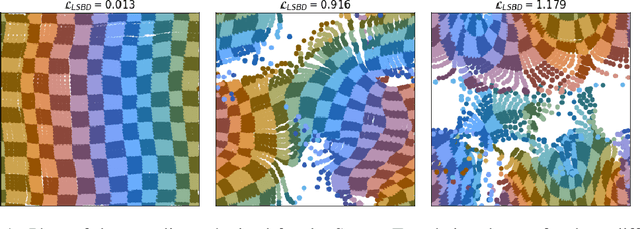
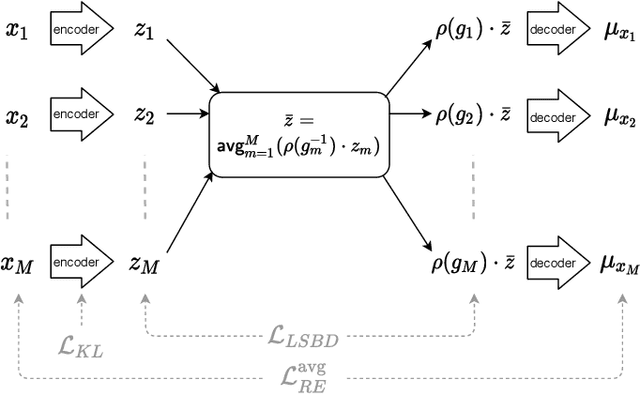
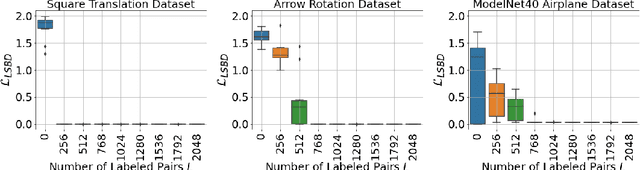
A Metric for Linear Symmetry-Based Disentanglement

The definition of Linear Symmetry-Based Disentanglement (LSBD) proposed by (Higgins et al., 2018) outlines the properties that should characterize a disentangled representation that captures the symmetries of data. However, it is not clear how to measure the degree to which a data representation fulfills these properties. We propose a metric for the evaluation of the level of LSBD that a data representation achieves. We provide a practical method to evaluate this metric and use it to evaluate the disentanglement of the data representations obtained for three datasets with underlying $SO(2)$ symmetries.

Disentanglement with Hyperspherical Latent Spaces using Diffusion Variational Autoencoders

A disentangled representation of a data set should be capable of recovering the underlying factors that generated it. One question that arises is whether using Euclidean space for latent variable models can produce a disentangled representation when the underlying generating factors have a certain geometrical structure. Take for example the images of a car seen from different angles. The angle has a periodic structure but a 1-dimensional representation would fail to capture this topology. How can we address this problem? The submissions presented for the first stage of the NeurIPS2019 Disentanglement Challenge consist of a Diffusion Variational Autoencoder ($\Delta$VAE) with a hyperspherical latent space which can, for example, recover periodic true factors. The training of the $\Delta$VAE is enhanced by incorporating a modified version of the Evidence Lower Bound (ELBO) for tailoring the encoding capacity of the posterior approximate.

Diffusion Variational Autoencoders

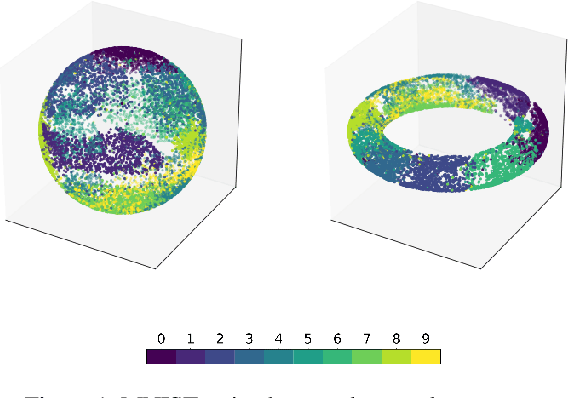
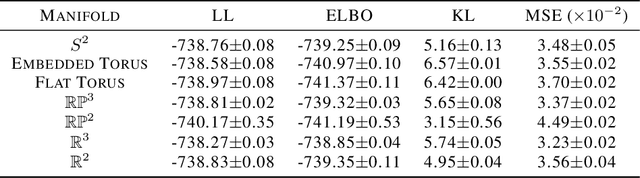
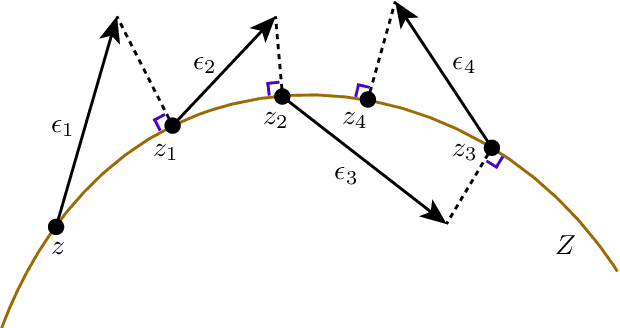
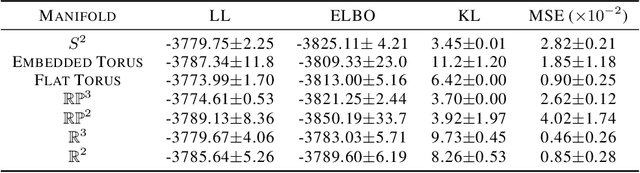
A standard Variational Autoencoder, with a Euclidean latent space, is structurally incapable of capturing topological properties of certain datasets. To remove topological obstructions, we introduce Diffusion Variational Autoencoders with arbitrary manifolds as a latent space. A Diffusion Variational Autoencoder uses transition kernels of Brownian motion on the manifold. In particular, it uses properties of the Brownian motion to implement the reparametrization trick and fast approximations to the KL divergence. We show that the Diffusion Variational Autoencoder is capable of capturing topological properties of synthetic datasets. Additionally, we train MNIST on spheres, tori, projective spaces, SO(3), and a torus embedded in R3. Although a natural dataset like MNIST does not have latent variables with a clear-cut topological structure, training it on a manifold can still highlight topological and geometrical properties.