Unrolling Plug-and-Play Network for Hyperspectral Unmixing

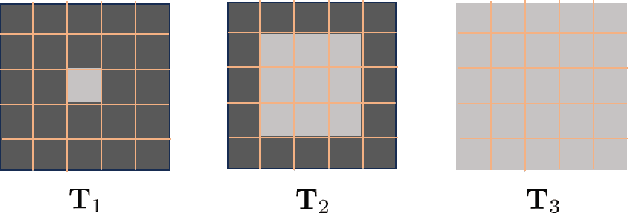
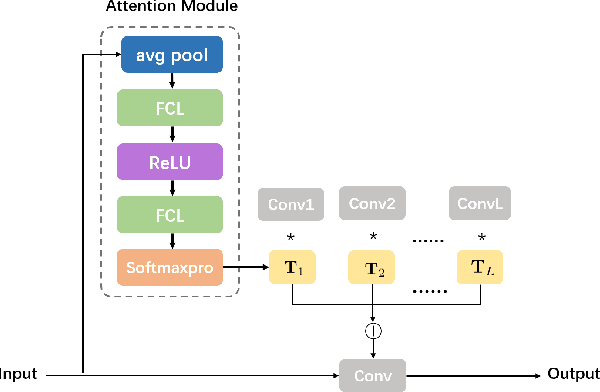
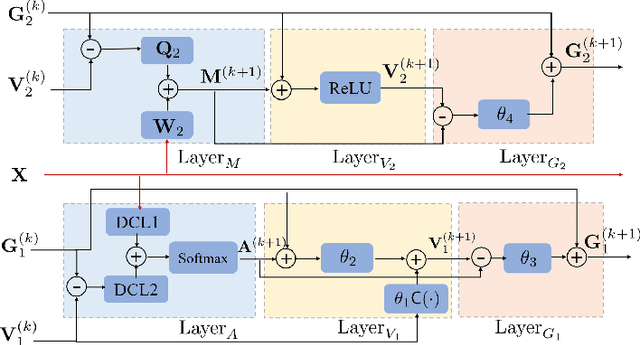
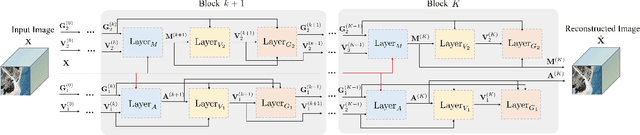
Deep learning based unmixing methods have received great attention in recent years and achieve remarkable performance. These methods employ a data-driven approach to extract structure features from hyperspectral image, however, they tend to be less physical interpretable. Conventional unmixing methods are with much more interpretability, whereas they require manually designing regularization and choosing penalty parameters. To overcome these limitations, we propose a novel unmixing method by unrolling the plug-and-play unmixing algorithm to conduct the deep architecture. Our method integrates both inner and outer priors. The carefully designed unfolding deep architecture is used to learn the spectral and spatial information from the hyperspectral image, which we refer to as inner priors. Additionally, our approach incorporates deep denoisers that have been pretrained on a large volume of image data to leverage the outer priors. Secondly, we design a dynamic convolution to model the multiscale information. Different scales are fused using an attention module. Experimental results of both synthetic and real datasets demonstrate that our method outperforms compared methods.

Wasserstein Nonnegative Tensor Factorization with Manifold Regularization

Nonnegative tensor factorization (NTF) has become an important tool for feature extraction and part-based representation with preserved intrinsic structure information from nonnegative high-order data. However, the original NTF methods utilize Euclidean or Kullback-Leibler divergence as the loss function which treats each feature equally leading to the neglect of the side-information of features. To utilize correlation information of features and manifold information of samples, we introduce Wasserstein manifold nonnegative tensor factorization (WMNTF), which minimizes the Wasserstein distance between the distribution of input tensorial data and the distribution of reconstruction. Although some researches about Wasserstein distance have been proposed in nonnegative matrix factorization (NMF), they ignore the spatial structure information of higher-order data. We use Wasserstein distance (a.k.a Earth Mover's distance or Optimal Transport distance) as a metric and add a graph regularizer to a latent factor. Experimental results demonstrate the effectiveness of the proposed method compared with other NMF and NTF methods.

Robust Manifold Nonnegative Tucker Factorization for Tensor Data Representation

Nonnegative Tucker Factorization (NTF) minimizes the euclidean distance or Kullback-Leibler divergence between the original data and its low-rank approximation which often suffers from grossly corruptions or outliers and the neglect of manifold structures of data. In particular, NTF suffers from rotational ambiguity, whose solutions with and without rotation transformations are equally in the sense of yielding the maximum likelihood. In this paper, we propose three Robust Manifold NTF algorithms to handle outliers by incorporating structural knowledge about the outliers. They first applies a half-quadratic optimization algorithm to transform the problem into a general weighted NTF where the weights are influenced by the outliers. Then, we introduce the correntropy induced metric, Huber function and Cauchy function for weights respectively, to handle the outliers. Finally, we introduce a manifold regularization to overcome the rotational ambiguity of NTF. We have compared the proposed method with a number of representative references covering major branches of NTF on a variety of real-world image databases. Experimental results illustrate the effectiveness of the proposed method under two evaluation metrics (accuracy and nmi).