Verifying Integrity of Deep Ensemble Models by Lossless Black-box Watermarking with Sensitive Samples

With the widespread use of deep neural networks (DNNs) in many areas, more and more studies focus on protecting DNN models from intellectual property (IP) infringement. Many existing methods apply digital watermarking to protect the DNN models. The majority of them either embed a watermark directly into the internal network structure/parameters or insert a zero-bit watermark by fine-tuning a model to be protected with a set of so-called trigger samples. Though these methods work very well, they were designed for individual DNN models, which cannot be directly applied to deep ensemble models (DEMs) that combine multiple DNN models to make the final decision. It motivates us to propose a novel black-box watermarking method in this paper for DEMs, which can be used for verifying the integrity of DEMs. In the proposed method, a certain number of sensitive samples are carefully selected through mimicking real-world DEM attacks and analyzing the prediction results of the sub-models of the non-attacked DEM and the attacked DEM on the carefully crafted dataset. By analyzing the prediction results of the target DEM on these carefully crafted sensitive samples, we are able to verify the integrity of the target DEM. Different from many previous methods, the proposed method does not modify the original DEM to be protected, which indicates that the proposed method is lossless. Experimental results have shown that the DEM integrity can be reliably verified even if only one sub-model was attacked, which has good potential in practice.

Statistical significance in high-dimensional linear mixed models

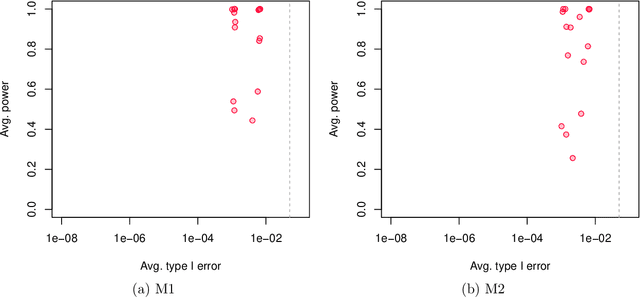
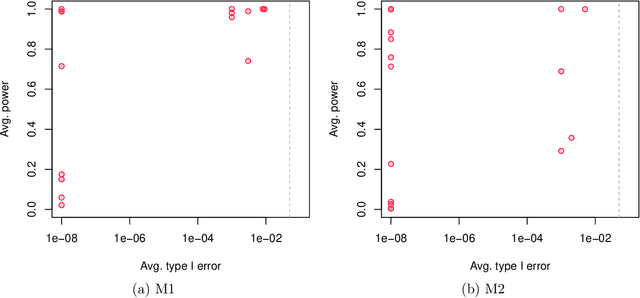
This paper concerns the development of an inferential framework for high-dimensional linear mixed effect models. These are suitable models, for instance, when we have $n$ repeated measurements for $M$ subjects. We consider a scenario where the number of fixed effects $p$ is large (and may be larger than $M$), but the number of random effects $q$ is small. Our framework is inspired by a recent line of work that proposes de-biasing penalized estimators to perform inference for high-dimensional linear models with fixed effects only. In particular, we demonstrate how to correct a `naive' ridge estimator in extension of work by B\"uhlmann (2013) to build asymptotically valid confidence intervals for mixed effect models. We validate our theoretical results with numerical experiments, in which we show our method outperforms those that fail to account for correlation induced by the random effects. For a practical demonstration we consider a riboflavin production dataset that exhibits group structure, and show that conclusions drawn using our method are consistent with those obtained on a similar dataset without group structure.