Statistical significance in high-dimensional linear mixed models
Paper and Code
Dec 16, 2019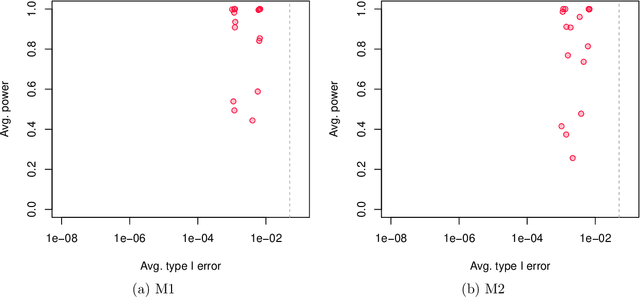
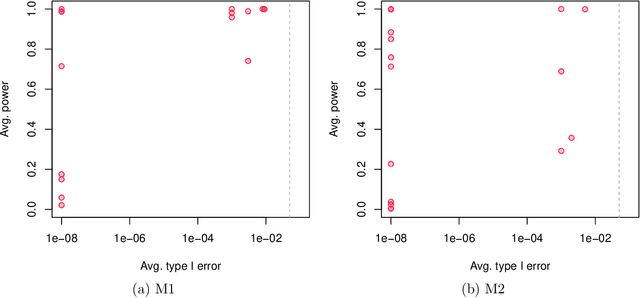


This paper concerns the development of an inferential framework for high-dimensional linear mixed effect models. These are suitable models, for instance, when we have $n$ repeated measurements for $M$ subjects. We consider a scenario where the number of fixed effects $p$ is large (and may be larger than $M$), but the number of random effects $q$ is small. Our framework is inspired by a recent line of work that proposes de-biasing penalized estimators to perform inference for high-dimensional linear models with fixed effects only. In particular, we demonstrate how to correct a `naive' ridge estimator in extension of work by B\"uhlmann (2013) to build asymptotically valid confidence intervals for mixed effect models. We validate our theoretical results with numerical experiments, in which we show our method outperforms those that fail to account for correlation induced by the random effects. For a practical demonstration we consider a riboflavin production dataset that exhibits group structure, and show that conclusions drawn using our method are consistent with those obtained on a similar dataset without group structure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge