A Deep-Learning Usability Expansion Model of Ocean Observations

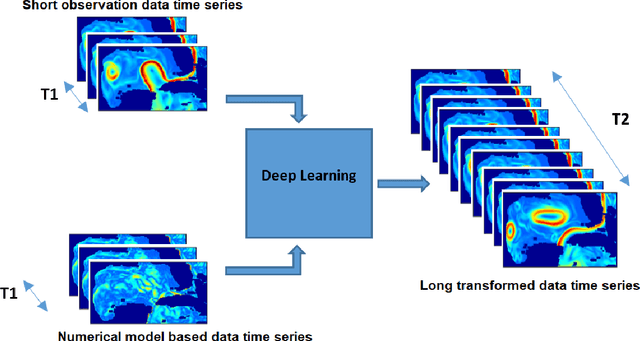
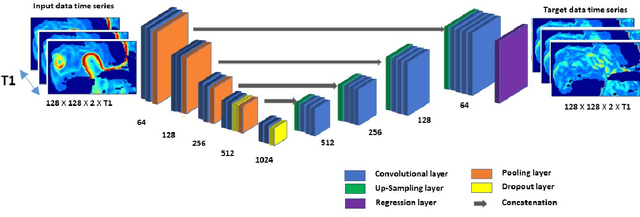
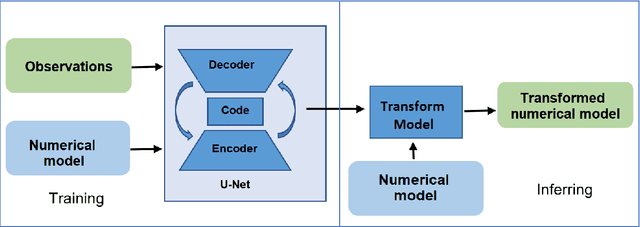
Today's ocean numerical prediction skills depend on the availability of in-situ and remote ocean observations at the time of the predictions only. Because observations are scarce and discontinuous in time and space, numerical models are often unable to accurately model and predict real ocean dynamics, leading to a lack of fulfillment of a range of services that require reliable predictions at various temporal and spatial scales. The process of constraining free numerical models with observations is known as data assimilation. The primary objective is to minimize the misfit of model states with the observations while respecting the rules of physics. The caveat of this approach is that measurements are used only once, at the time of the prediction. The information contained in the history of the measurements and its role in the determinism of the prediction is, therefore, not accounted for. Consequently, historical measurement cannot be used in real-time forecasting systems. The research presented in this paper provides a novel approach rooted in artificial intelligence to expand the usability of observations made before the time of the prediction. Our approach is based on the re-purpose of an existing deep learning model, called U-Net, designed specifically for image segmentation analysis in the biomedical field. U-Net is used here to create a Transform Model that retains the temporal and spatial evolution of the differences between model and observations to produce a correction in the form of regression weights that evolves spatially and temporally with the model both forward and backward in time, beyond the observation period. Using virtual observations, we show that the usability of the observation can be extended up to a one year prior or post observations.

ST-PCNN: Spatio-Temporal Physics-Coupled Neural Networks for Dynamics Forecasting

Ocean current, fluid mechanics, and many other spatio-temporal physical dynamical systems are essential components of the universe. One key characteristic of such systems is that certain physics laws -- represented as ordinary/partial differential equations (ODEs/PDEs) -- largely dominate the whole process, irrespective of time or location. Physics-informed learning has recently emerged to learn physics for accurate prediction, but they often lack a mechanism to leverage localized spatial and temporal correlation or rely on hard-coded physics parameters. In this paper, we advocate a physics-coupled neural network model to learn parameters governing the physics of the system, and further couple the learned physics to assist the learning of recurring dynamics. A spatio-temporal physics-coupled neural network (ST-PCNN) model is proposed to achieve three goals: (1) learning the underlying physics parameters, (2) transition of local information between spatio-temporal regions, and (3) forecasting future values for the dynamical system. The physics-coupled learning ensures that the proposed model can be tremendously improved by using learned physics parameters, and can achieve good long-range forecasting (e.g., more than 30-steps). Experiments, using simulated and field-collected ocean current data, validate that ST-PCNN outperforms existing physics-informed models.