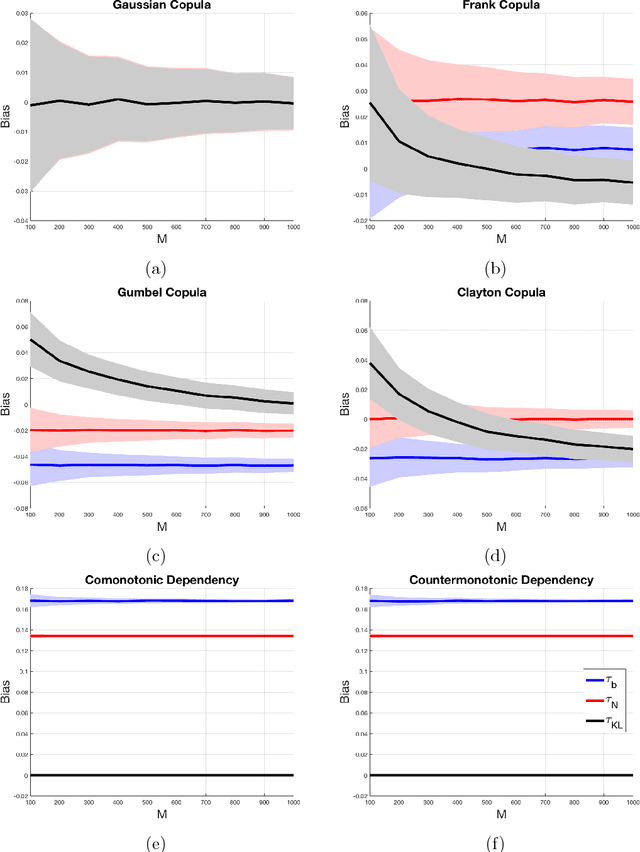
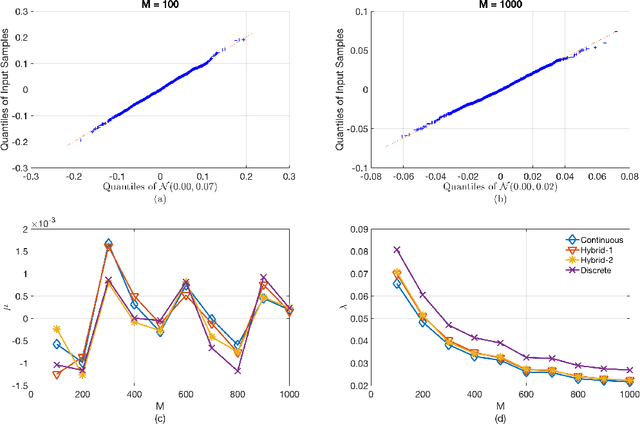
Kullback-Leibler Divergence-Guided Copula Statistics-Based Blind Source Separation of Dependent Signals

In this paper, we propose a blind source separation of a linear mixture of dependent sources based on copula statistics that measure the non-linear dependence between source component signals structured as copula density functions. The source signals are assumed to be stationary. The method minimizes the Kullback-Leibler divergence between the copula density functions of the estimated sources and of the dependency structure. The proposed method is applied to data obtained from the time-domain analysis of the classical 11-Bus 4-Machine system. Extensive simulation results demonstrate that the proposed method based on copula statistics converges faster and outperforms the state-of-the-art blind source separation method for dependent sources in terms of interference-to-signal ratio.

Identification of Power System Oscillation Modes using Blind Source Separation based on Copula Statistic

The dynamics of a power system with large penetration of renewable energy resources are becoming more nonlinear due to the intermittence of these resources and the switching of their power electronic devices. Therefore, it is crucial to accurately identify the dynamical modes of oscillation of such a power system when it is subject to disturbances to initiate appropriate preventive or corrective control actions. In this paper, we propose a high-order blind source identification (HOBI) algorithm based on the copula statistic to address these non-linear dynamics in modal analysis. The method combined with Hilbert transform (HOBI-HT) and iteration procedure (HOBMI) can identify all the modes as well as the model order from the observation signals obtained from the number of channels as low as one. We access the performance of the proposed method on numerical simulation signals and recorded data from a simulation of time domain analysis on the classical 11-Bus 4-Machine test system. Our simulation results outperform the state-of-the-art method in accuracy and effectiveness.

Robust Gaussian Process Regression with Huber Likelihood

Gaussian process regression in its most simplified form assumes normal homoscedastic noise and utilizes analytically tractable mean and covariance functions of predictive posterior distribution using Gaussian conditioning. Its hyperparameters are estimated by maximizing the evidence, commonly known as type II maximum likelihood estimation. Unfortunately, Bayesian inference based on Gaussian likelihood is not robust to outliers, which are often present in the observational training data sets. To overcome this problem, we propose a robust process model in the Gaussian process framework with the likelihood of observed data expressed as the Huber probability distribution. The proposed model employs weights based on projection statistics to scale residuals and bound the influence of vertical outliers and bad leverage points on the latent functions estimates while exhibiting a high statistical efficiency at the Gaussian and thick tailed noise distributions. The proposed method is demonstrated by two real world problems and two numerical examples using datasets with additive errors following thick tailed distributions such as Students t, Laplace, and Cauchy distribution.

A Robust Data-driven Process Modeling Applied to Time-series Stochastic Power Flow

In this paper, we propose a robust data-driven process model whose hyperparameters are robustly estimated using the Schweppe-type generalized maximum likelihood estimator. The proposed model is trained on recorded time-series data of voltage phasors and power injections to perform a time-series stochastic power flow calculation. Power system data are often corrupted with outliers caused by large errors, fault conditions, power outages, and extreme weather, to name a few. The proposed model downweights vertical outliers and bad leverage points in the measurements of the training dataset. The weights used to bound the influence of the outliers are calculated using projection statistics, which are a robust version of Mahalanobis distances of the time series data points. The proposed method is demonstrated on the IEEE 33-Bus power distribution system and a real-world unbalanced 240-bus power distribution system heavily integrated with renewable energy sources. Our simulation results show that the proposed robust model can handle up to 25% of outliers in the training data set.

Robust Dynamic Mode Decomposition

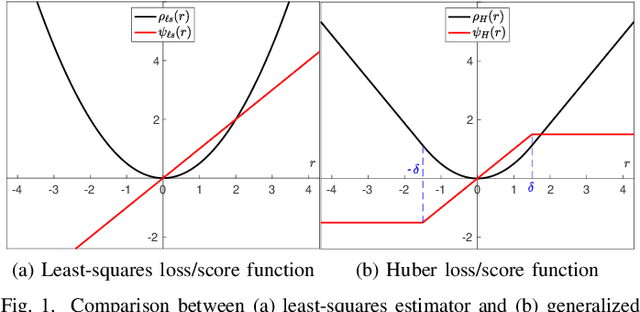
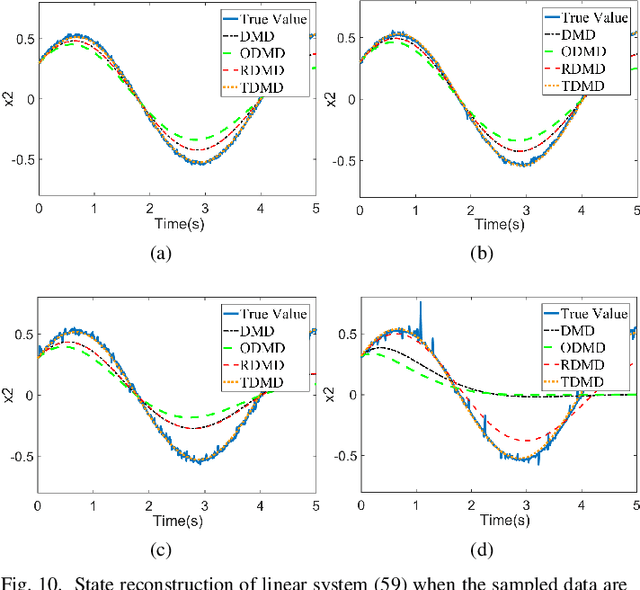
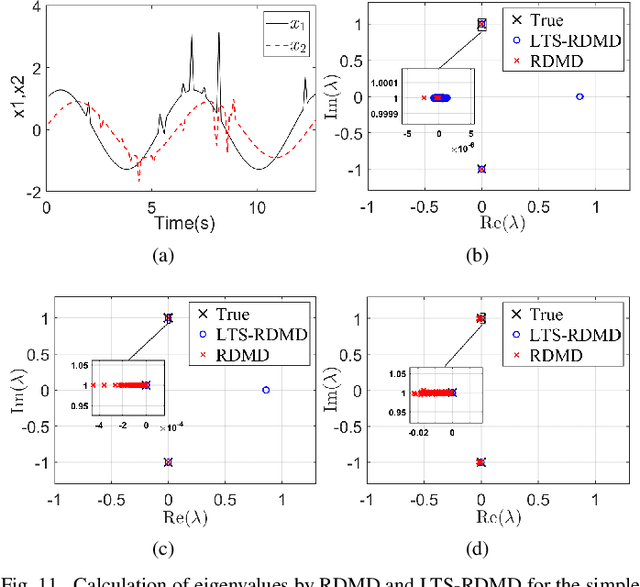
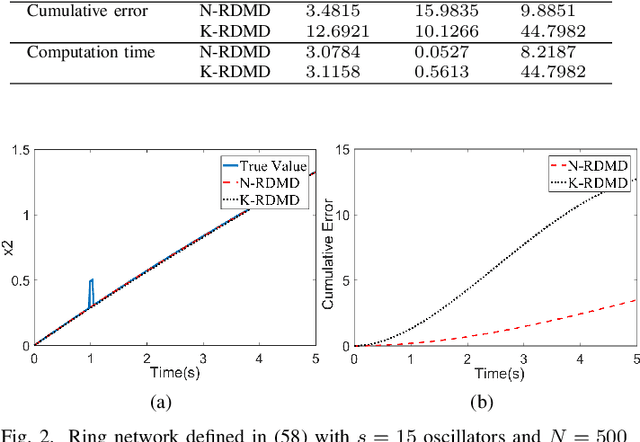
The paper develops a robust estimation method that makes the dynamic mode decomposition method resistant to outliers while being fast to compute and statistically efficient (i.e. accurate) at the Gaussian and non-Gaussian thick tailed distributions. The proposed robust dynamic mode decomposition (RDMD) is anchored on the theory of robust statistics. Specifically, it relies on the Schweppe-type Huber generalized maximum-likelihood estimator that minimizes a convex weighted Huber loss function, where the weights are calculated via projection statistics, thereby making the proposed RDMD robust to outliers, whether vertical outliers or bad leverage points. The performance of the proposed RDMD is demonstrated numerically using canonical models of dynamical systems. Simulation results reveal that it outperforms several other methods proposed in the literature.

Copula Index for Detecting Dependence and Monotonicity between Stochastic Signals

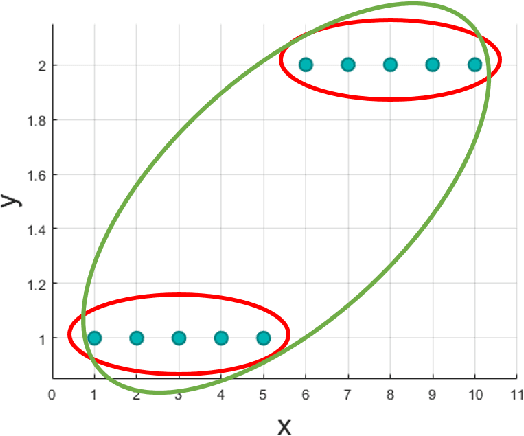
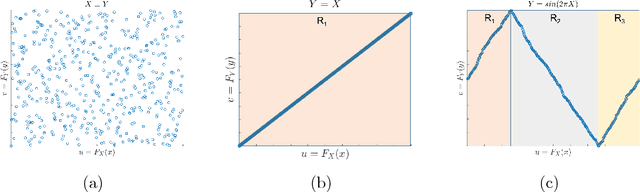
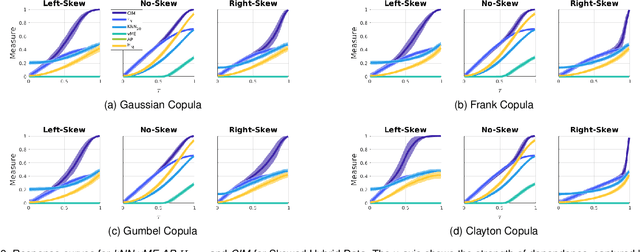
This paper introduces a nonparametric copula-based index for detecting the strength and monotonicity structure of linear and nonlinear statistical dependence between pairs of random variables or stochastic signals. Our index, termed Copula Index for Detecting Dependence and Monotonicity (CIM), satisfies several desirable properties of measures of association, including Renyi's properties, the data processing inequality (DPI), and consequently self-equitability. Synthetic data simulations reveal that the statistical power of CIM compares favorably to other state-of-the-art measures of association that are proven to satisfy the DPI. Simulation results with real-world data reveal the CIM's unique ability to detect the monotonicity structure among stochastic signals to find interesting dependencies in large datasets. Additionally, simulations show that the CIM shows favorable performance to estimators of mutual information when discovering Markov network structure.

On the Effect of Suboptimal Estimation of Mutual Information in Feature Selection and Classification

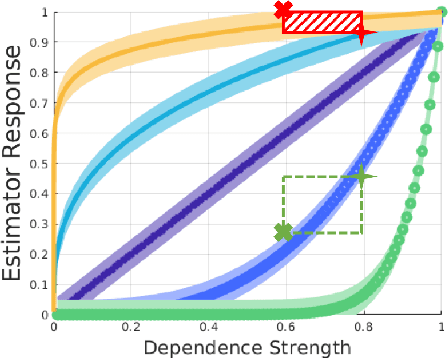
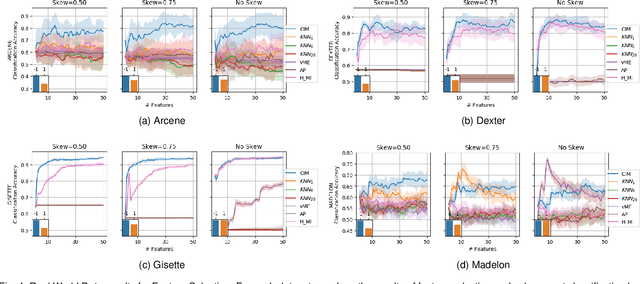
This paper introduces a new property of estimators of the strength of statistical association, which helps characterize how well an estimator will perform in scenarios where dependencies between continuous and discrete random variables need to be rank ordered. The new property, termed the estimator response curve, is easily computable and provides a marginal distribution agnostic way to assess an estimator's performance. It overcomes notable drawbacks of current metrics of assessment, including statistical power, bias, and consistency. We utilize the estimator response curve to test various measures of the strength of association that satisfy the data processing inequality (DPI), and show that the CIM estimator's performance compares favorably to kNN, vME, AP, and H_{MI} estimators of mutual information. The estimators which were identified to be suboptimal, according to the estimator response curve, perform worse than the more optimal estimators when tested with real-world data from four different areas of science, all with varying dimensionalities and sizes.