Robust Dynamic Mode Decomposition

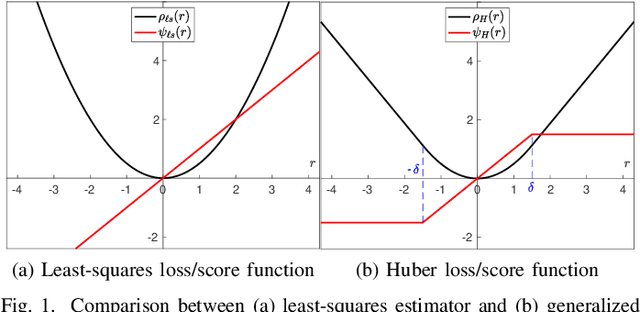
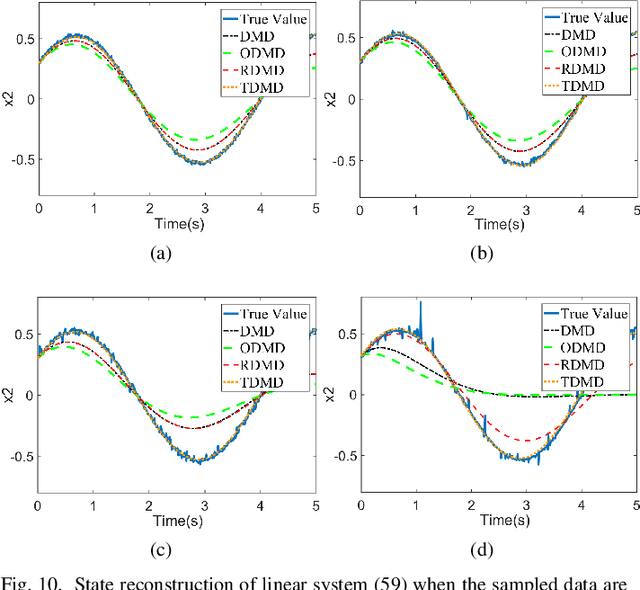
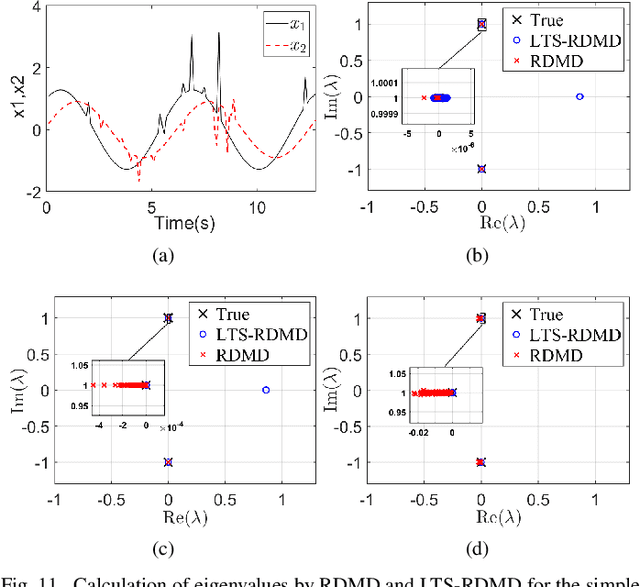
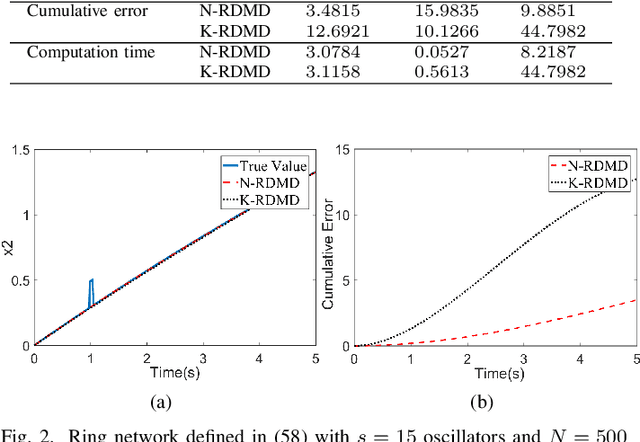
The paper develops a robust estimation method that makes the dynamic mode decomposition method resistant to outliers while being fast to compute and statistically efficient (i.e. accurate) at the Gaussian and non-Gaussian thick tailed distributions. The proposed robust dynamic mode decomposition (RDMD) is anchored on the theory of robust statistics. Specifically, it relies on the Schweppe-type Huber generalized maximum-likelihood estimator that minimizes a convex weighted Huber loss function, where the weights are calculated via projection statistics, thereby making the proposed RDMD robust to outliers, whether vertical outliers or bad leverage points. The performance of the proposed RDMD is demonstrated numerically using canonical models of dynamical systems. Simulation results reveal that it outperforms several other methods proposed in the literature.