Superior generalization of smaller models in the presence of significant label noise

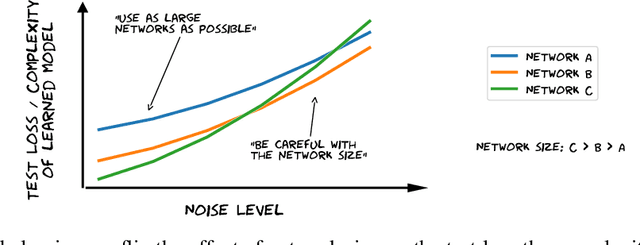
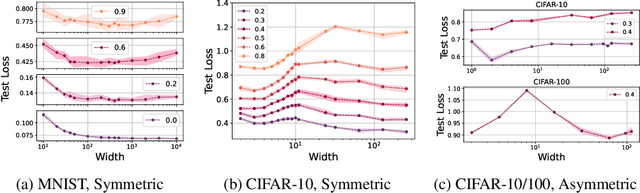
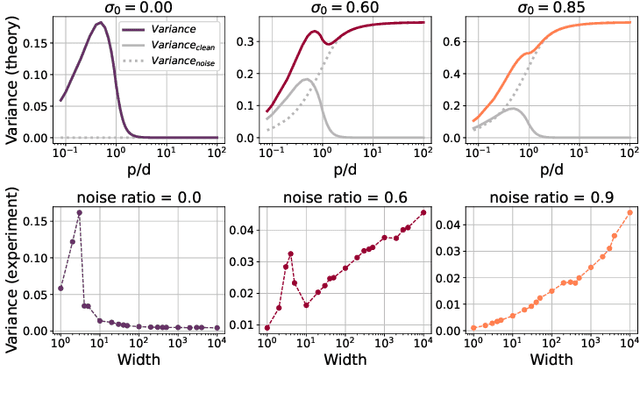
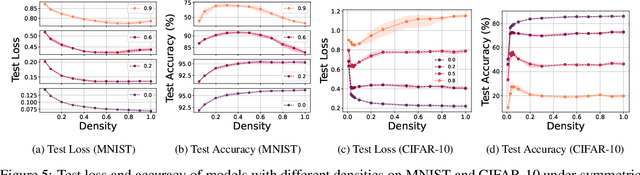
The benefits of over-parameterization in achieving superior generalization performance have been shown in several recent studies, justifying the trend of using larger models in practice. In the context of robust learning however, the effect of neural network size has not been well studied. In this work, we find that in the presence of a substantial fraction of mislabeled examples, increasing the network size beyond some point can be harmful. In particular, the originally monotonic or `double descent' test loss curve (w.r.t. network width) turns into a U-shaped or a double U-shaped curve when label noise increases, suggesting that the best generalization is achieved by some model with intermediate size. We observe that when network size is controlled by density through random pruning, similar test loss behaviour is observed. We also take a closer look into both phenomenon through bias-variance decomposition and theoretically characterize how label noise shapes the variance term. Similar behavior of the test loss can be observed even when state-of-the-art robust methods are applied, indicating that limiting the network size could further boost existing methods. Finally, we empirically examine the effect of network size on the smoothness of learned functions, and find that the originally negative correlation between size and smoothness is flipped by label noise.

Investigating Why Contrastive Learning Benefits Robustness Against Label Noise

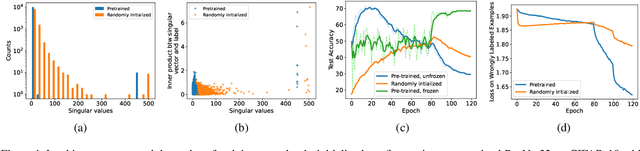
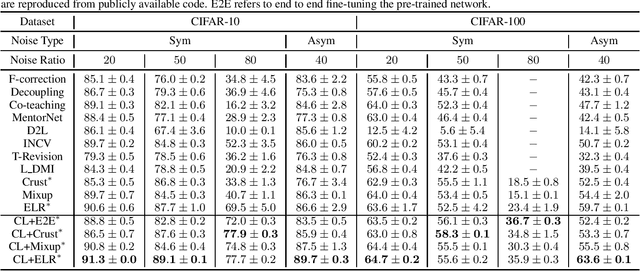
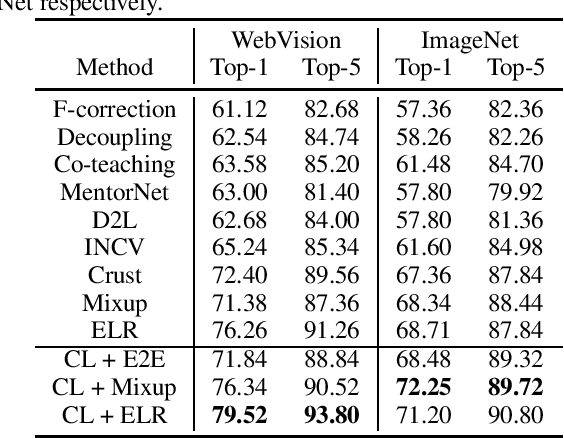
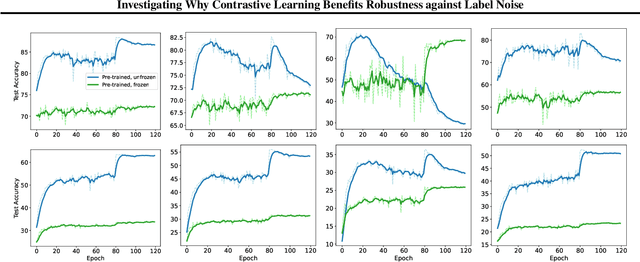
Self-supervised contrastive learning has recently been shown to be very effective in preventing deep networks from overfitting noisy labels. Despite its empirical success, the theoretical understanding of the effect of contrastive learning on boosting robustness is very limited. In this work, we rigorously prove that the representation matrix learned by contrastive learning boosts robustness, by having: (i) one prominent singular value corresponding to every sub-class in the data, and remaining significantly smaller singular values; and (ii) a large alignment between the prominent singular vector and the clean labels of each sub-class. The above properties allow a linear layer trained on the representations to quickly learn the clean labels, and prevent it from overfitting the noise for a large number of training iterations. We further show that the low-rank structure of the Jacobian of deep networks pre-trained with contrastive learning allows them to achieve a superior performance initially, when fine-tuned on noisy labels. Finally, we demonstrate that the initial robustness provided by contrastive learning enables robust training methods to achieve state-of-the-art performance under extreme noise levels, e.g., an average of 27.18\% and 15.58\% increase in accuracy on CIFAR-10 and CIFAR-100 with 80\% symmetric noisy labels, and 4.11\% increase in accuracy on WebVision.