Superior generalization of smaller models in the presence of significant label noise
Paper and Code
Aug 17, 2022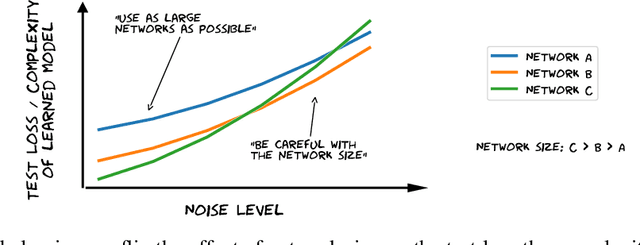
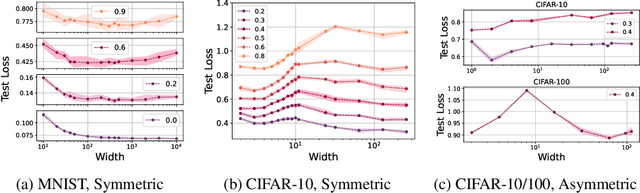
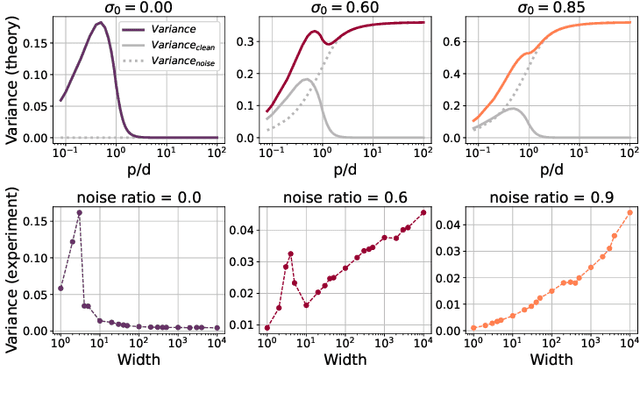
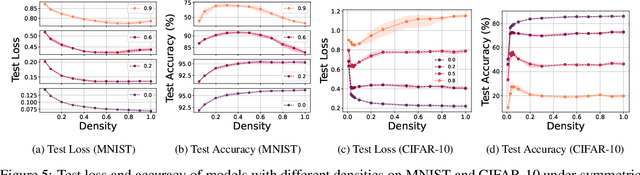
The benefits of over-parameterization in achieving superior generalization performance have been shown in several recent studies, justifying the trend of using larger models in practice. In the context of robust learning however, the effect of neural network size has not been well studied. In this work, we find that in the presence of a substantial fraction of mislabeled examples, increasing the network size beyond some point can be harmful. In particular, the originally monotonic or `double descent' test loss curve (w.r.t. network width) turns into a U-shaped or a double U-shaped curve when label noise increases, suggesting that the best generalization is achieved by some model with intermediate size. We observe that when network size is controlled by density through random pruning, similar test loss behaviour is observed. We also take a closer look into both phenomenon through bias-variance decomposition and theoretically characterize how label noise shapes the variance term. Similar behavior of the test loss can be observed even when state-of-the-art robust methods are applied, indicating that limiting the network size could further boost existing methods. Finally, we empirically examine the effect of network size on the smoothness of learned functions, and find that the originally negative correlation between size and smoothness is flipped by label noise.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge