Generative adversarial neural networks for simulating neutrino interactions

We propose a new approach to simulate neutrino scattering events as an alternative to the standard Monte Carlo generator approach. Generative adversarial neural network (GAN) models are developed to simulate neutrino-carbon collisions in the few-GeV energy range. The models produce scattering events for a given neutrino energy. GAN models are trained on simulation data from NuWro Monte Carlo event generator. Two GAN models have been obtained: one simulating only quasielastic neutrino-nucleus scatterings and another simulating all interactions at given neutrino energy. The performance of both models has been assessed using two statistical metrics. It is shown that both GAN models successfully reproduce the event distributions.

Electron-nucleus cross sections from transfer learning

Transfer learning (TL) allows a deep neural network (DNN) trained on one type of data to be adapted for new problems with limited information. We propose to use the TL technique in physics. The DNN learns the physics of one process, and after fine-tuning, it makes predictions for related processes. We consider the DNNs, trained on inclusive electron-carbon scattering data, and show that after fine-tuning, they accurately predict cross sections for electron interactions with nuclear targets ranging from lithium to iron. The method works even when the DNN is fine-tuned on a small dataset.

Empirical fits to inclusive electron-carbon scattering data obtained by deep-learning methods

Employing the neural network framework, we obtain empirical fits to the electron-scattering cross section for carbon over a broad kinematic region, extending from the quasielastic peak, through resonance excitation, to the onset of deep-inelastic scattering. We consider two different methods of obtaining such model-independent parametrizations and the corresponding uncertainties: based on the NNPDF approach [J. High Energy Phys. 2002, 062], and on the Monte Carlo dropout. In our analysis, the $\chi^2$ function defines the loss function, including point-to-point uncertainties and considering the systematic normalization uncertainties for each independent set of measurements. Our statistical approaches lead to fits of comparable quality and similar uncertainties of the order of $7\%$ and $12\%$ for the first and the second approaches, respectively. To test these models, we compare their predictions to a~test dataset, excluded from the training process, a~dataset lying beyond the covered kinematic region, and theoretical predictions obtained within the spectral function approach. The predictions of both models agree with experimental measurements and the theoretical predictions. However, the first statistical approach shows better interpolation and extrapolation abilities than the one based on the dropout algorithm.

Bayesian Reasoning for Physics Informed Neural Networks

Physics informed neural network (PINN) approach in Bayesian formulation is presented. We adopt the Bayesian neural network framework formulated by MacKay (Neural Computation 4 (3) (1992) 448). The posterior densities are obtained from Laplace approximation. For each model (fit), the so-called evidence is computed. It is a measure that classifies the hypothesis. The most optimal solution has the maximal value of the evidence. The Bayesian framework allows us to control the impact of the boundary contribution to the total loss. Indeed, the relative weights of loss components are fine-tuned by the Bayesian algorithm. We solve heat, wave, and Burger's equations. The obtained results are in good agreement with the exact solutions. All solutions are provided with the uncertainties computed within the Bayesian framework.

Deep learning for diffusion in porous media

We adopt convolutional neural networks (CNN) to predict the basic properties of the porous media. Two different media types are considered: one mimics the sandstone, and the other mimics the systems derived from the extracellular space of biological tissues. The Lattice Boltzmann Method is used to obtain the labeled data necessary for performing supervised learning. We distinguish two tasks. In the first, networks based on the analysis of the system's geometry predict porosity and effective diffusion coefficient. In the second, networks reconstruct the system's geometry and concentration map. In the first task, we propose two types of CNN models: the C-Net and the encoder part of the U-Net. Both networks are modified by adding a self-normalization module. The models predict with reasonable accuracy but only within the data type, they are trained on. For instance, the model trained on sandstone-like samples overshoots or undershoots for biological-like samples. In the second task, we propose the usage of the U-Net architecture. It accurately reconstructs the concentration fields. Moreover, the network trained on one data type works well for the other. For instance, the model trained on sandstone-like samples works perfectly on biological-like samples.

Self-Normalized Density Map (SNDM) for Counting Microbiological Objects

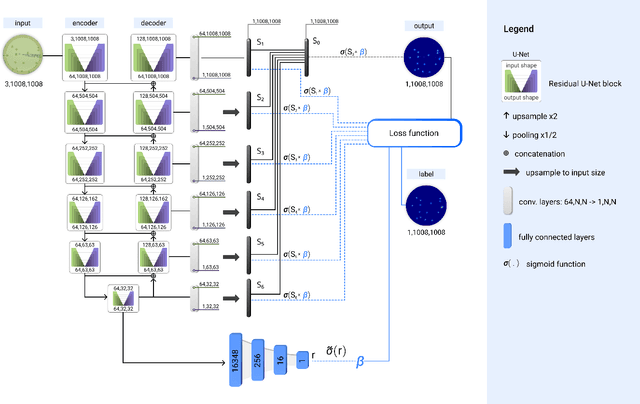
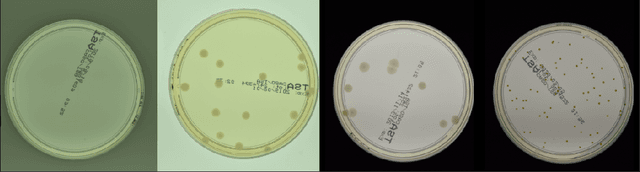
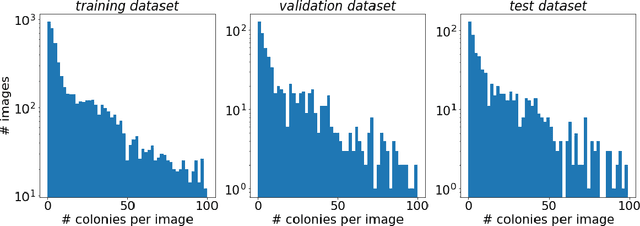
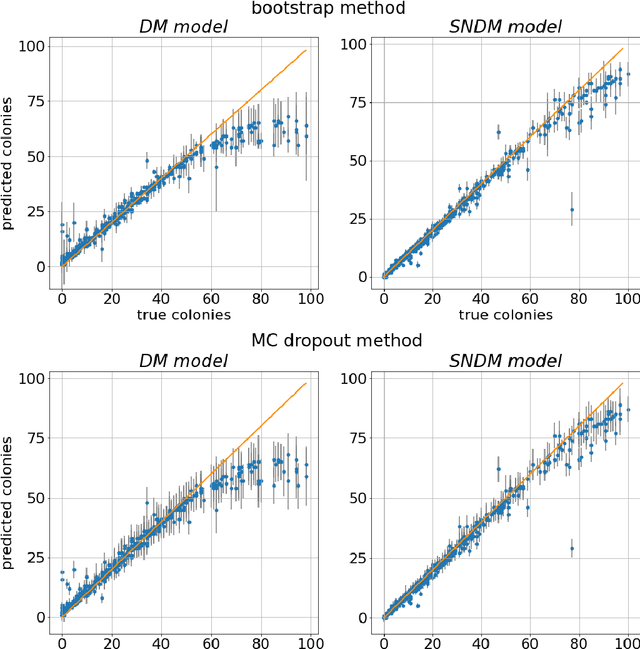
The statistical properties of the density map (DM) approach to counting microbiological objects on images are studied in detail. The DM is given by U$^2$-Net. Two statistical methods for deep neural networks are utilized: the bootstrap and the Monte Carlo (MC) dropout. The detailed analysis of the uncertainties for the DM predictions leads to a deeper understanding of the DM model's deficiencies. Based on our investigation, we propose a self-normalization module in the network. The improved network model, called Self-Normalized Density Map (SNDM), can correct its output density map by itself to accurately predict the total number of objects in the image. The SNDM architecture outperforms the original model. Moreover, both statistical frameworks -- bootstrap and MC dropout -- have consistent statistical results for SNDM, which were not observed in the original model.

Predicting Porosity, Permeability, and Tortuosity of Porous Media from Images by Deep Learning

Convolutional neural networks (CNN) are utilized to encode the relation between initial configurations of obstacles and three fundamental quantities in porous media: porosity ($\varphi$), permeability $k$, and tortuosity ($T$). The two-dimensional systems with obstacles are considered. The fluid flow through a porous medium is simulated with the lattice Boltzmann method. It is demonstrated that the CNNs are able to predict the porosity, permeability, and tortuosity with good accuracy. With the usage of the CNN models, the relation between $T$ and $\varphi$ has been reproduced and compared with the empirical estimate. The analysis has been performed for the systems with $\varphi \in (0.37,0.99)$ which covers five orders of magnitude span for permeability $k \in (0.78, 2.1\times 10^5)$ and tortuosity $T \in (1.03,2.74)$.