Collision Probabilities for Continuous-Time Systems Without Sampling [with Appendices]

Demand for high-performance, robust, and safe autonomous systems has grown substantially in recent years. Fulfillment of these objectives requires accurate and efficient risk estimation that can be embedded in core decision-making tasks such as motion planning. On one hand, Monte-Carlo (MC) and other sampling-based techniques can provide accurate solutions for a wide variety of motion models but are cumbersome to apply in the context of continuous optimization. On the other hand, "direct" approximations aim to compute (or upper-bound) the failure probability as a smooth function of the decision variables, and thus are widely applicable. However, existing approaches fundamentally assume discrete-time dynamics and can perform unpredictably when applied to continuous-time systems operating in the real world, often manifesting as severe conservatism. State-of-the-art attempts to address this within a conventional discrete-time framework require additional Gaussianity approximations that ultimately produce inconsistency of their own. In this paper we take a fundamentally different approach, deriving a risk approximation framework directly in continuous time and producing a lightweight estimate that actually improves as the discretization is refined. Our approximation is shown to significantly outperform state-of-the-art techniques in replicating the MC estimate while maintaining the functional and computational benefits of a direct method. This enables robust, risk-aware, continuous motion-planning for a broad class of nonlinear, partially-observable systems.

Towards Online Observability-Aware Trajectory Optimization for Landmark-based Estimators

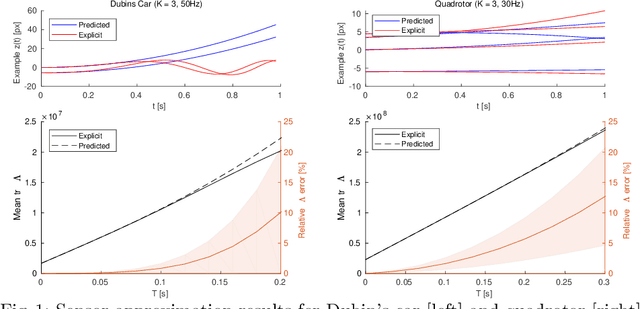
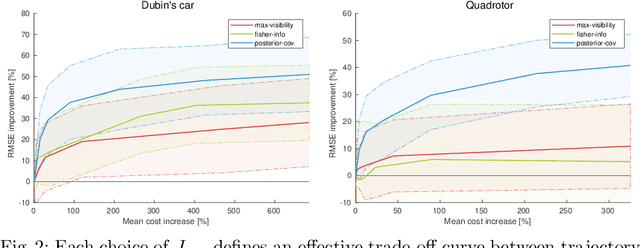
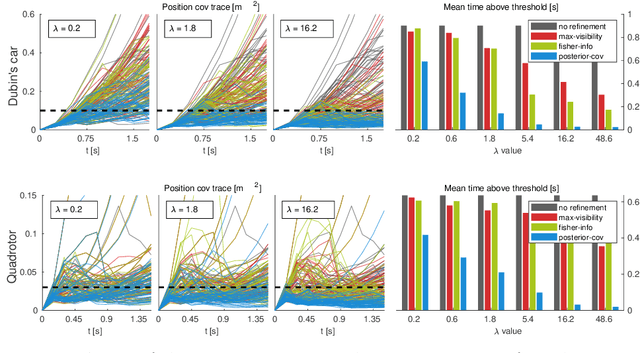
As autonomous systems rely increasingly on onboard sensors for localization and perception, the parallel tasks of motion planning and uncertainty minimization become increasingly coupled. This coupling is well-captured by augmenting the planning objective with a posterior-covariance penalty -- however, online optimization can be computationally intractable, particularly for observation models with latent environmental dependencies (e.g., unknown landmarks). This paper addresses a number of fundamental challenges in efficient minimization of the posterior covariance. First, we provide a measurement bundling approximation that enables high-rate sensors to be approximated with fewer, low-rate updates. This allows for landmark marginalization (crucial in the case of unknown landmarks), for which we provide a novel recipe for computing the gradients necessary for optimization. Finally, we identify a large class of measurement models for which the contributions from each landmark can be combined, so evaluation of the total information gained at each timestep can be carried out (nearly) independently of the number of landmarks. We evaluate our trajectory-generation framework for both a Dubin's car and a quadrotor, demonstrating significant estimation improvement and moderate computation time.

Efficient Constellation-Based Map-Merging for Semantic SLAM

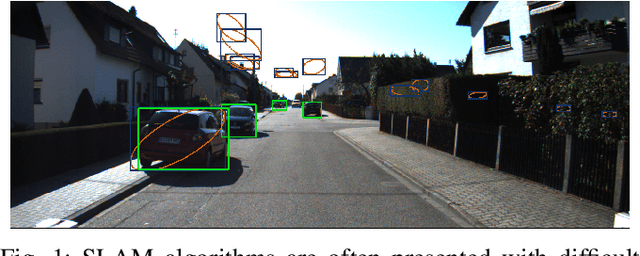
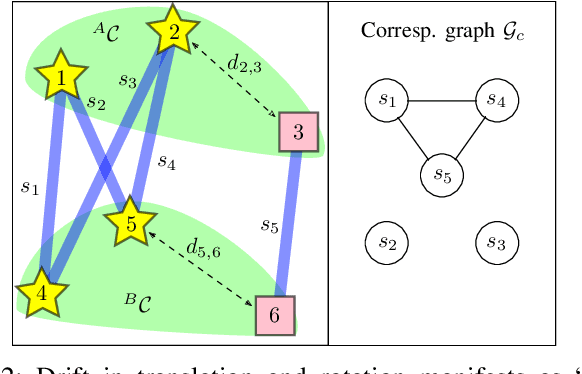
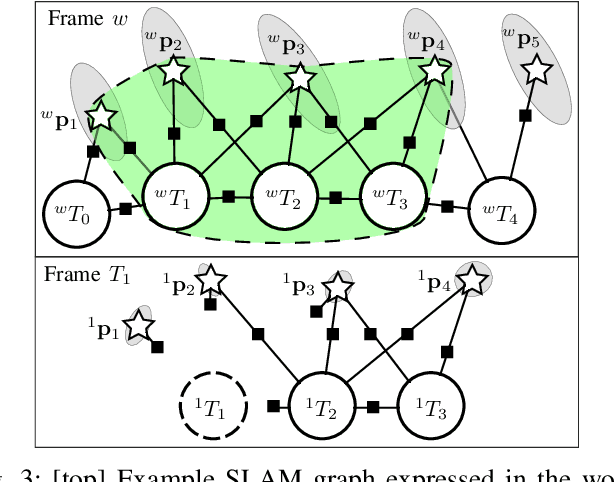
Data association in SLAM is fundamentally challenging, and handling ambiguity well is crucial to achieve robust operation in real-world environments. When ambiguous measurements arise, conservatism often mandates that the measurement is discarded or a new landmark is initialized rather than risking an incorrect association. To address the inevitable `duplicate' landmarks that arise, we present an efficient map-merging framework to detect duplicate constellations of landmarks, providing a high-confidence loop-closure mechanism well-suited for object-level SLAM. This approach uses an incrementally-computable approximation of landmark uncertainty that only depends on local information in the SLAM graph, avoiding expensive recovery of the full system covariance matrix. This enables a search based on geometric consistency (GC) (rather than full joint compatibility (JC)) that inexpensively reduces the search space to a handful of `best' hypotheses. Furthermore, we reformulate the commonly-used interpretation tree to allow for more efficient integration of clique-based pairwise compatibility, accelerating the branch-and-bound max-cardinality search. Our method is demonstrated to match the performance of full JC methods at significantly-reduced computational cost, facilitating robust object-based loop-closure over large SLAM problems.

Complexity Analysis and Efficient Measurement Selection Primitives for High-Rate Graph SLAM

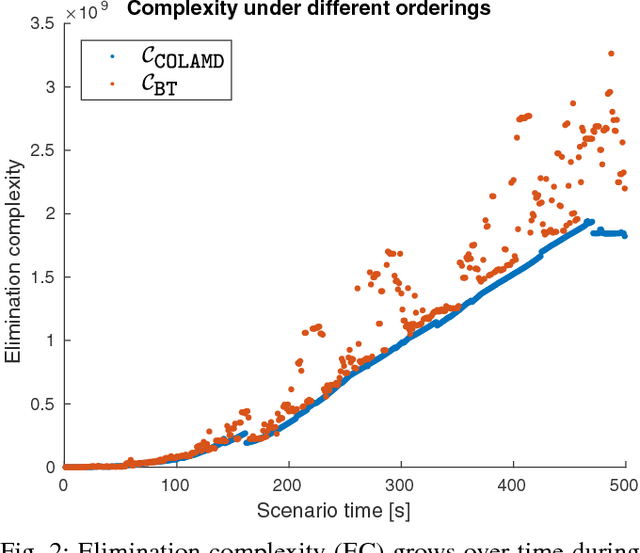
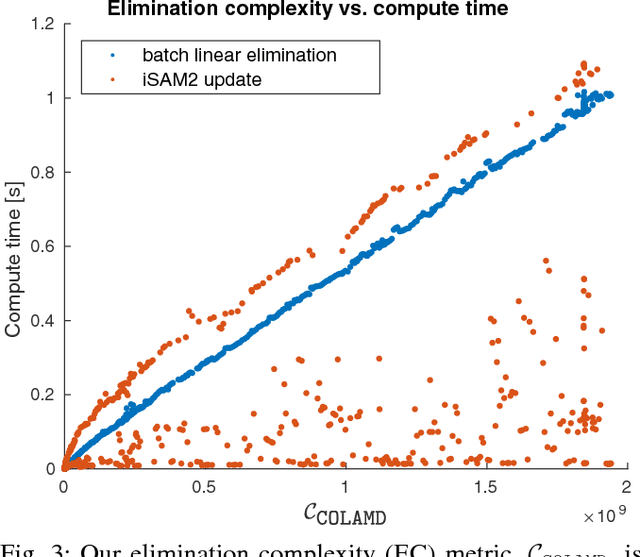
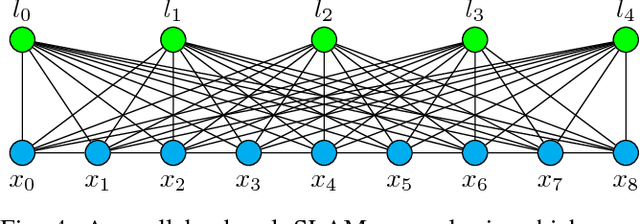
Sparsity has been widely recognized as crucial for efficient optimization in graph-based SLAM. Because the sparsity and structure of the SLAM graph reflect the set of incorporated measurements, many methods for sparsification have been proposed in hopes of reducing computation. These methods often focus narrowly on reducing edge count without regard for structure at a global level. Such structurally-naive techniques can fail to produce significant computational savings, even after aggressive pruning. In contrast, simple heuristics such as measurement decimation and keyframing are known empirically to produce significant computation reductions. To demonstrate why, we propose a quantitative metric called elimination complexity (EC) that bridges the existing analytic gap between graph structure and computation. EC quantifies the complexity of the primary computational bottleneck: the factorization step of a Gauss-Newton iteration. Using this metric, we show rigorously that decimation and keyframing impose favorable global structures and therefore achieve computation reductions on the order of $r^2/9$ and $r^3$, respectively, where $r$ is the pruning rate. We additionally present numerical results showing EC provides a good approximation of computation in both batch and incremental (iSAM2) optimization and demonstrate that pruning methods promoting globally-efficient structure outperform those that do not.