Towards Online Observability-Aware Trajectory Optimization for Landmark-based Estimators

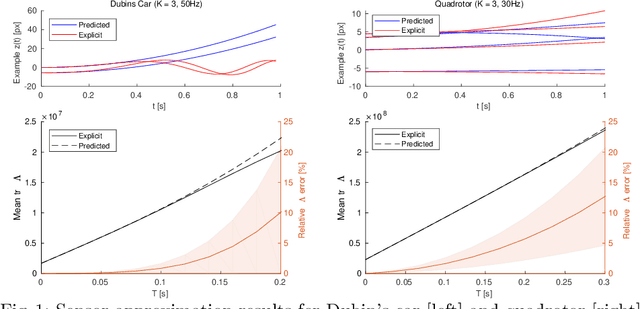
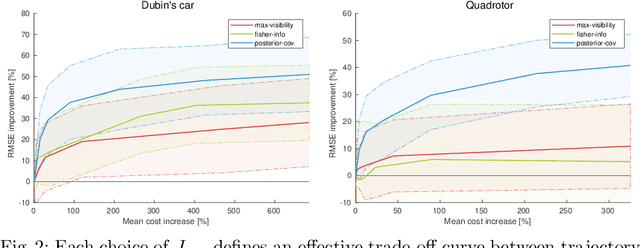
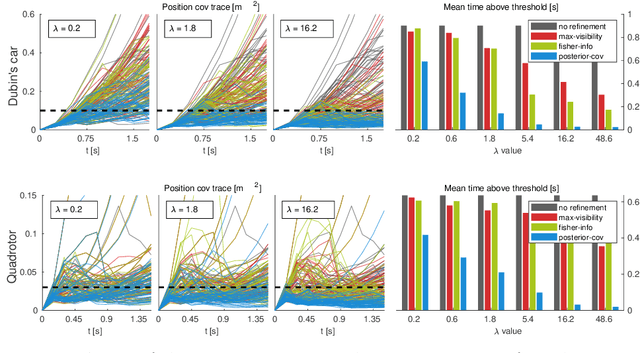
As autonomous systems rely increasingly on onboard sensors for localization and perception, the parallel tasks of motion planning and uncertainty minimization become increasingly coupled. This coupling is well-captured by augmenting the planning objective with a posterior-covariance penalty -- however, online optimization can be computationally intractable, particularly for observation models with latent environmental dependencies (e.g., unknown landmarks). This paper addresses a number of fundamental challenges in efficient minimization of the posterior covariance. First, we provide a measurement bundling approximation that enables high-rate sensors to be approximated with fewer, low-rate updates. This allows for landmark marginalization (crucial in the case of unknown landmarks), for which we provide a novel recipe for computing the gradients necessary for optimization. Finally, we identify a large class of measurement models for which the contributions from each landmark can be combined, so evaluation of the total information gained at each timestep can be carried out (nearly) independently of the number of landmarks. We evaluate our trajectory-generation framework for both a Dubin's car and a quadrotor, demonstrating significant estimation improvement and moderate computation time.