Kostadin Koroutchev
Thermodynamics of Information Retrieval
Feb 27, 2011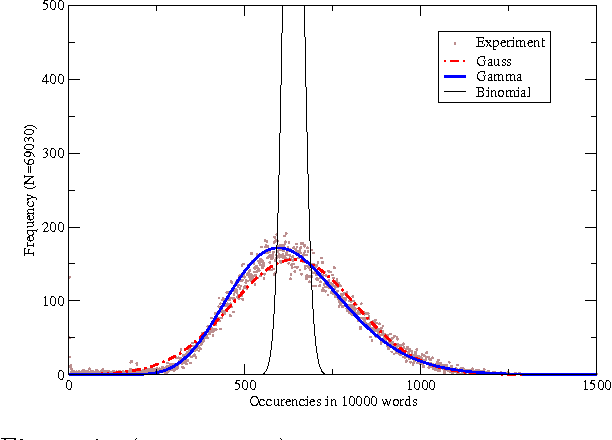
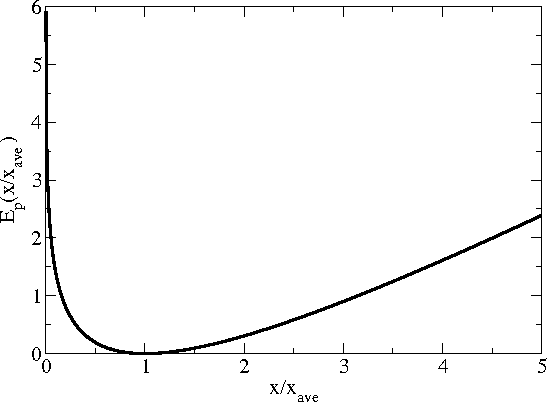
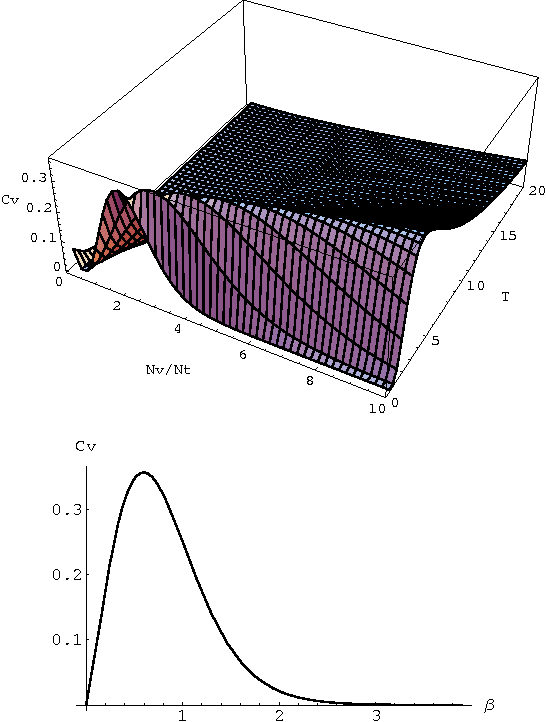
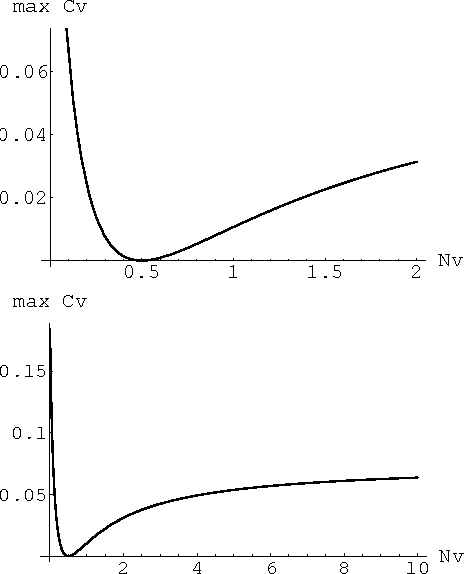
Abstract:In this work, we suggest a parameterized statistical model (the gamma distribution) for the frequency of word occurrences in long strings of English text and use this model to build a corresponding thermodynamic picture by constructing the partition function. We then use our partition function to compute thermodynamic quantities such as the free energy and the specific heat. In this approach, the parameters of the word frequency model vary from word to word so that each word has a different corresponding thermodynamics and we suggest that differences in the specific heat reflect differences in how the words are used in language, differentiating keywords from common and function words. Finally, we apply our thermodynamic picture to the problem of retrieval of texts based on keywords and suggest some advantages over traditional information retrieval methods.
Detecting the Most Unusual Part of Two and Three-dimensional Digital Images
May 05, 2010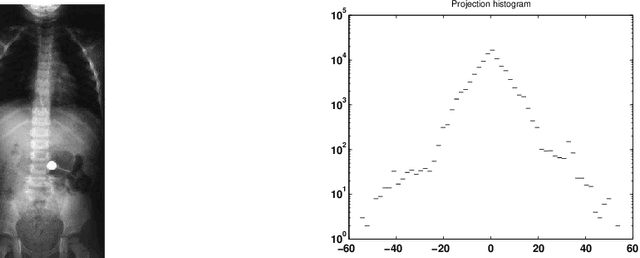
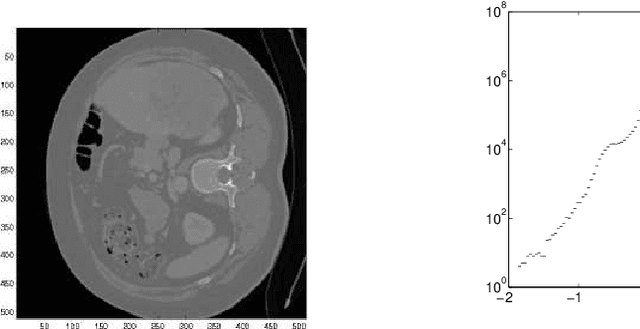


Abstract:The purpose of this paper is to introduce an algorithm that can detect the most unusual part of a digital image in probabilistic setting. The most unusual part of a given shape is defined as a part of the image that has the maximal distance to all non intersecting shapes with the same form. The method is tested on two and three-dimensional images and has shown very good results without any predefined model. A version of the method independent of the contrast of the image is considered and is found to be useful for finding the most unusual part (and the most similar part) of the image conditioned on given image. The results can be used to scan large image databases, as for example medical databases.
* 16 pages
Dynamical Neural Network: Information and Topology
Jun 20, 2005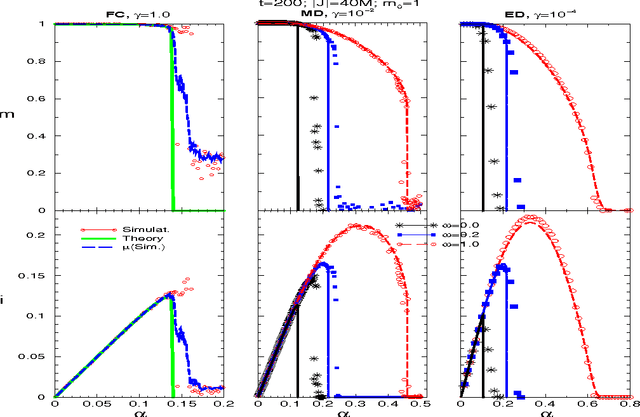
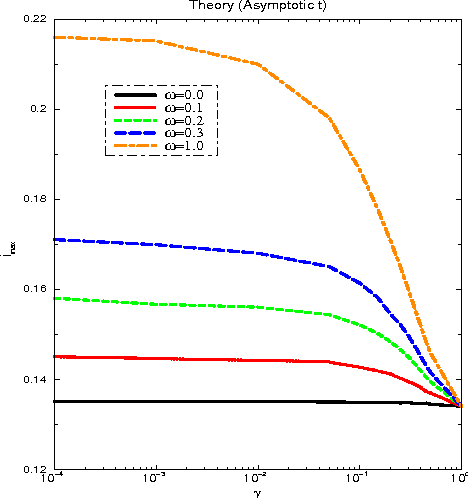
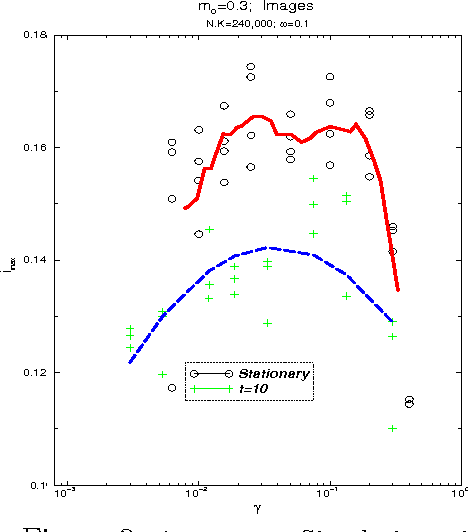
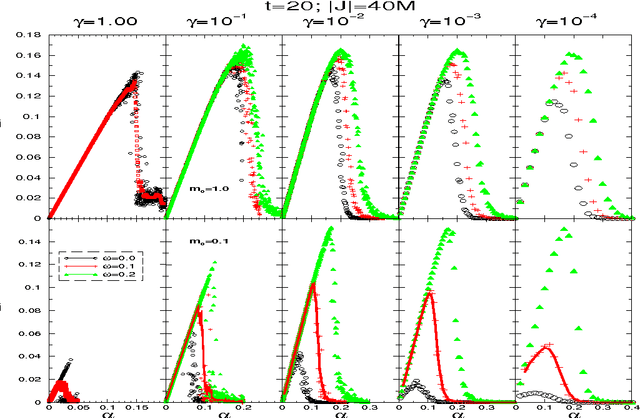
Abstract:A neural network works as an associative memory device if it has large storage capacity and the quality of the retrieval is good enough. The learning and attractor abilities of the network both can be measured by the mutual information (MI), between patterns and retrieval states. This paper deals with a search for an optimal topology, of a Hebb network, in the sense of the maximal MI. We use small-world topology. The connectivity $\gamma$ ranges from an extremely diluted to the fully connected network; the randomness $\omega$ ranges from purely local to completely random neighbors. It is found that, while stability implies an optimal $MI(\gamma,\omega)$ at $\gamma_{opt}(\omega)\to 0$, for the dynamics, the optimal topology holds at certain $\gamma_{opt}>0$ whenever $0\leq\omega<0.3$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge