Accurate and robust image superresolution by neural processing of local image representations

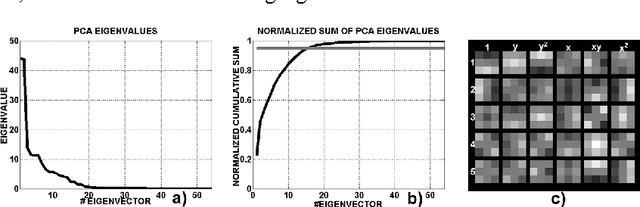
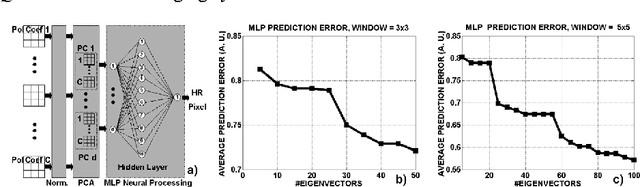
Image superresolution involves the processing of an image sequence to generate a still image with higher resolution. Classical approaches, such as bayesian MAP methods, require iterative minimization procedures, with high computational costs. Recently, the authors proposed a method to tackle this problem, based on the use of a hybrid MLP-PNN architecture. In this paper, we present a novel superresolution method, based on an evolution of this concept, to incorporate the use of local image models. A neural processing stage receives as input the value of model coefficients on local windows. The data dimensionality is firstly reduced by application of PCA. An MLP, trained on synthetic sequences with various amounts of noise, estimates the high-resolution image data. The effect of varying the dimension of the network input space is examined, showing a complex, structured behavior. Quantitative results are presented showing the accuracy and robustness of the proposed method.

Dynamical Neural Network: Information and Topology

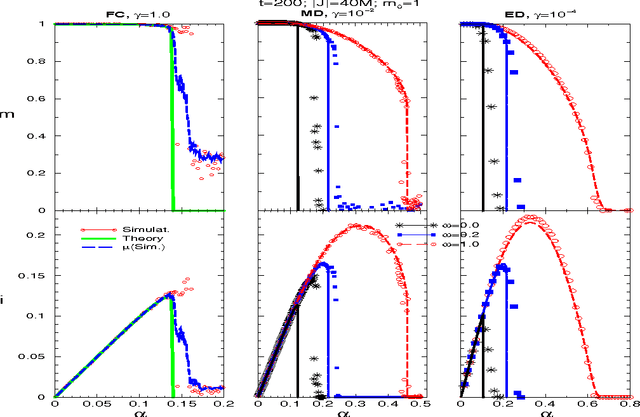
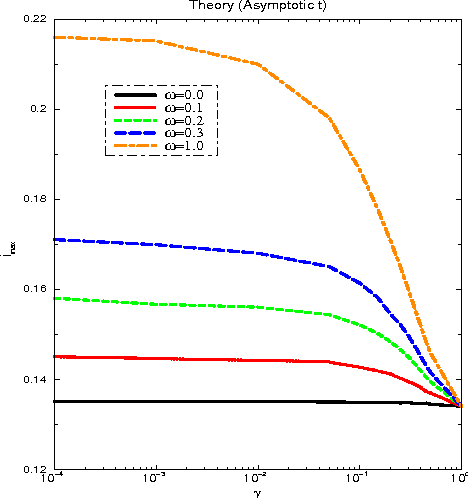
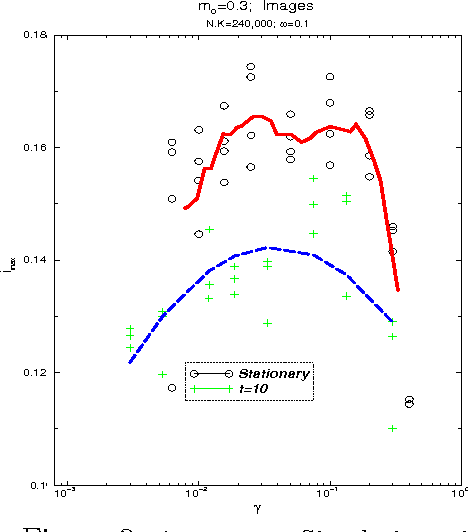
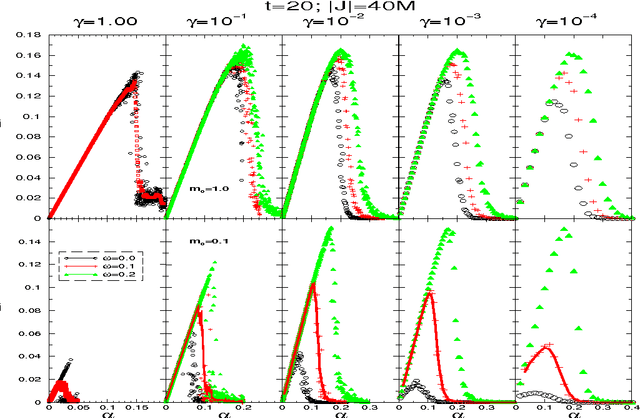
A neural network works as an associative memory device if it has large storage capacity and the quality of the retrieval is good enough. The learning and attractor abilities of the network both can be measured by the mutual information (MI), between patterns and retrieval states. This paper deals with a search for an optimal topology, of a Hebb network, in the sense of the maximal MI. We use small-world topology. The connectivity $\gamma$ ranges from an extremely diluted to the fully connected network; the randomness $\omega$ ranges from purely local to completely random neighbors. It is found that, while stability implies an optimal $MI(\gamma,\omega)$ at $\gamma_{opt}(\omega)\to 0$, for the dynamics, the optimal topology holds at certain $\gamma_{opt}>0$ whenever $0\leq\omega<0.3$.

A hybrid MLP-PNN architecture for fast image superresolution

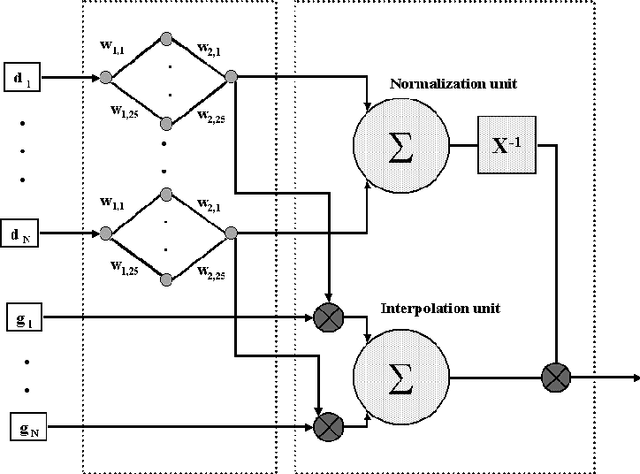
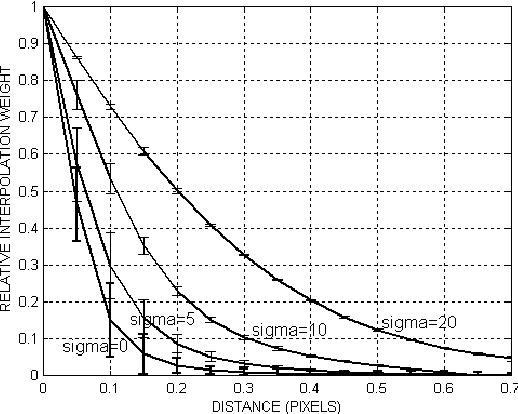
Image superresolution methods process an input image sequence of a scene to obtain a still image with increased resolution. Classical approaches to this problem involve complex iterative minimization procedures, typically with high computational costs. In this paper is proposed a novel algorithm for super-resolution that enables a substantial decrease in computer load. First, a probabilistic neural network architecture is used to perform a scattered-point interpolation of the image sequence data. The network kernel function is optimally determined for this problem by a multi-layer perceptron trained on synthetic data. Network parameters dependence on sequence noise level is quantitatively analyzed. This super-sampled image is spatially filtered to correct finite pixel size effects, to yield the final high-resolution estimate. Results on a real outdoor sequence are presented, showing the quality of the proposed method.