A Split-Merge Framework for Comparing Clusterings

Clustering evaluation measures are frequently used to evaluate the performance of algorithms. However, most measures are not properly normalized and ignore some information in the inherent structure of clusterings. We model the relation between two clusterings as a bipartite graph and propose a general component-based decomposition formula based on the components of the graph. Most existing measures are examples of this formula. In order to satisfy consistency in the component, we further propose a split-merge framework for comparing clusterings of different data sets. Our framework gives measures that are conditionally normalized, and it can make use of data point information, such as feature vectors and pairwise distances. We use an entropy-based instance of the framework and a coreference resolution data set to demonstrate empirically the utility of our framework over other measures.

Optimizing F-measure: A Tale of Two Approaches

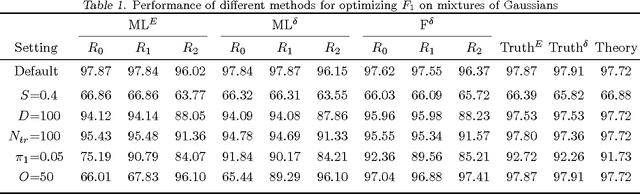
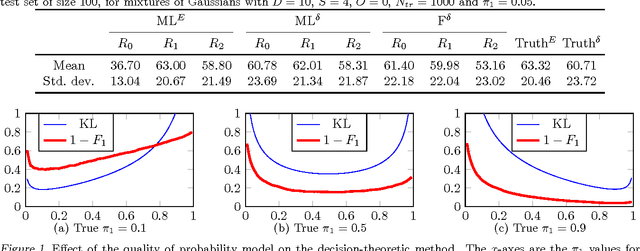
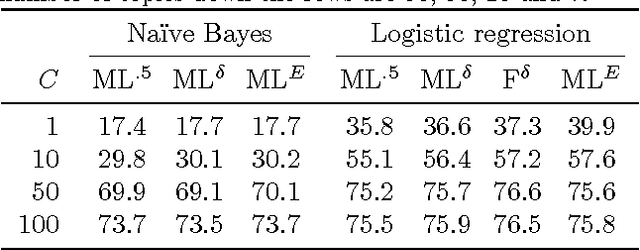
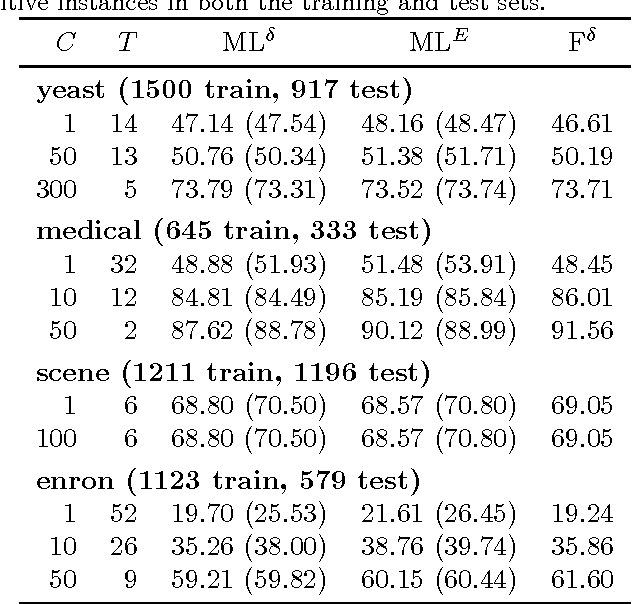
F-measures are popular performance metrics, particularly for tasks with imbalanced data sets. Algorithms for learning to maximize F-measures follow two approaches: the empirical utility maximization (EUM) approach learns a classifier having optimal performance on training data, while the decision-theoretic approach learns a probabilistic model and then predicts labels with maximum expected F-measure. In this paper, we investigate the theoretical justifications and connections for these two approaches, and we study the conditions under which one approach is preferable to the other using synthetic and real datasets. Given accurate models, our results suggest that the two approaches are asymptotically equivalent given large training and test sets. Nevertheless, empirically, the EUM approach appears to be more robust against model misspecification, and given a good model, the decision-theoretic approach appears to be better for handling rare classes and a common domain adaptation scenario.