Rao-Blackwellised Reparameterisation Gradients

Latent Gaussian variables have been popularised in probabilistic machine learning. In turn, gradient estimators are the machinery that facilitates gradient-based optimisation for models with latent Gaussian variables. The reparameterisation trick is often used as the default estimator as it is simple to implement and yields low-variance gradients for variational inference. In this work, we propose the R2-G2 estimator as the Rao-Blackwellisation of the reparameterisation gradient estimator. Interestingly, we show that the local reparameterisation gradient estimator for Bayesian MLPs is an instance of the R2-G2 estimator and Rao-Blackwellisation. This lets us extend benefits of Rao-Blackwellised gradients to a suite of probabilistic models. We show that initial training with R2-G2 consistently yields better performance in models with multiple applications of the reparameterisation trick.

LegendreTron: Uprising Proper Multiclass Loss Learning

Loss functions serve as the foundation of supervised learning and are often chosen prior to model development. To avoid potentially ad hoc choices of losses, statistical decision theory describes a desirable property for losses known as \emph{properness}, which asserts that Bayes' rule is optimal. Recent works have sought to \emph{learn losses} and models jointly. Existing methods do this by fitting an inverse canonical link function which monotonically maps $\mathbb{R}$ to $[0,1]$ to estimate probabilities for binary problems. In this paper, we extend monotonicity to maps between $\mathbb{R}^{C-1}$ and the projected probability simplex $\tilde{\Delta}^{C-1}$ by using monotonicity of gradients of convex functions. We present {\sc LegendreTron} as a novel and practical method that jointly learns \emph{proper canonical losses} and probabilities for multiclass problems. Tested on a benchmark of domains with up to 1,000 classes, our experimental results show that our method consistently outperforms the natural multiclass baseline under a $t$-test at 99% significance on all datasets with greater than 10 classes.

Constraint-based Formation of Drone Swarms

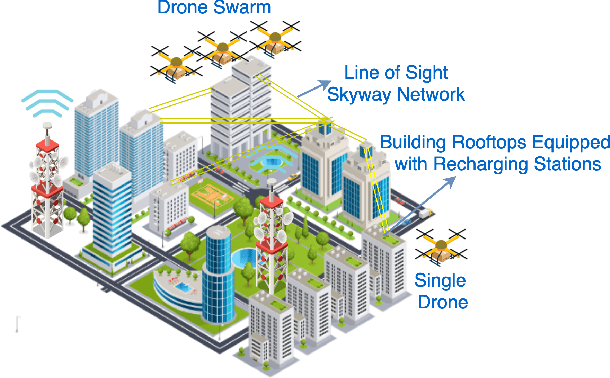
Drone swarms are required for the simultaneous delivery of multiple packages. We demonstrate a multi-stop drone swarm-based delivery in a smart city. We leverage formation flying to conserve energy and increase the flight range of a drone swarm. An adaptive formation is presented in which a swarm adjusts to extrinsic constraints and changes the formation pattern in-flight. We utilize the existing building rooftops in a city and build a line-of-sight skyway network to safely operate the swarms. We use a heuristic-based A* algorithm to route a drone swarm in a skyway network.