Mean-Field Assisted Deep Boltzmann Learning with Probabilistic Computers

Despite their appeal as physics-inspired, energy-based and generative nature, general Boltzmann Machines (BM) are considered intractable to train. This belief led to simplified models of BMs with restricted intralayer connections or layer-by-layer training of deep BMs. Recent developments in domain-specific hardware -- specifically probabilistic computers (p-computer) with probabilistic bits (p-bit) -- may change established wisdom on the tractability of deep BMs. In this paper, we show that deep and unrestricted BMs can be trained using p-computers generating hundreds of billions of Markov Chain Monte Carlo (MCMC) samples per second, on sparse networks developed originally for use in D-Wave's annealers. To maximize the efficiency of learning the p-computer, we introduce two families of Mean-Field Theory assisted learning algorithms, or xMFTs (x = Naive and Hierarchical). The xMFTs are used to estimate the averages and correlations during the positive phase of the contrastive divergence (CD) algorithm and our custom-designed p-computer is used to estimate the averages and correlations in the negative phase. A custom Field-Programmable-Gate Array (FPGA) emulation of the p-computer architecture takes up to 45 billion flips per second, allowing the implementation of CD-$n$ where $n$ can be of the order of millions, unlike RBMs where $n$ is typically 1 or 2. Experiments on the full MNIST dataset with the combined algorithm show that the positive phase can be efficiently computed by xMFTs without much degradation when the negative phase is computed by the p-computer. Our algorithm can be used in other scalable Ising machines and its variants can be used to train BMs, previously thought to be intractable.

Machine Learning Quantum Systems with Magnetic p-bits

The slowing down of Moore's Law has led to a crisis as the computing workloads of Artificial Intelligence (AI) algorithms continue skyrocketing. There is an urgent need for scalable and energy-efficient hardware catering to the unique requirements of AI algorithms and applications. In this environment, probabilistic computing with p-bits emerged as a scalable, domain-specific, and energy-efficient computing paradigm, particularly useful for probabilistic applications and algorithms. In particular, spintronic devices such as stochastic magnetic tunnel junctions (sMTJ) show great promise in designing integrated p-computers. Here, we examine how a scalable probabilistic computer with such magnetic p-bits can be useful for an emerging field combining machine learning and quantum physics.

CMOS + stochastic nanomagnets: heterogeneous computers for probabilistic inference and learning

Extending Moore's law by augmenting complementary-metal-oxide semiconductor (CMOS) transistors with emerging nanotechnologies (X) has become increasingly important. Accelerating Monte Carlo algorithms that rely on random sampling with such CMOS+X technologies could have significant impact on a large number of fields from probabilistic machine learning, optimization to quantum simulation. In this paper, we show the combination of stochastic magnetic tunnel junction (sMTJ)-based probabilistic bits (p-bits) with versatile Field Programmable Gate Arrays (FPGA) to design a CMOS + X (X = sMTJ) prototype. Our approach enables high-quality true randomness that is essential for Monte Carlo based probabilistic sampling and learning. Our heterogeneous computer successfully performs probabilistic inference and asynchronous Boltzmann learning, despite device-to-device variations in sMTJs. A comprehensive comparison using a CMOS predictive process design kit (PDK) reveals that compact sMTJ-based p-bits replace 10,000 transistors while dissipating two orders of magnitude of less energy (2 fJ per random bit), compared to digital CMOS p-bits. Scaled and integrated versions of our CMOS + stochastic nanomagnet approach can significantly advance probabilistic computing and its applications in various domains by providing massively parallel and truly random numbers with extremely high throughput and energy-efficiency.

Training Deep Boltzmann Networks with Sparse Ising Machines

The slowing down of Moore's law has driven the development of unconventional computing paradigms, such as specialized Ising machines tailored to solve combinatorial optimization problems. In this paper, we show a new application domain for probabilistic bit (p-bit) based Ising machines by training deep generative AI models with them. Using sparse, asynchronous, and massively parallel Ising machines we train deep Boltzmann networks in a hybrid probabilistic-classical computing setup. We use the full MNIST dataset without any downsampling or reduction in hardware-aware network topologies implemented in moderately sized Field Programmable Gate Arrays (FPGA). Our machine, which uses only 4,264 nodes (p-bits) and about 30,000 parameters, achieves the same classification accuracy (90%) as an optimized software-based restricted Boltzmann Machine (RBM) with approximately 3.25 million parameters. Additionally, the sparse deep Boltzmann network can generate new handwritten digits, a task the 3.25 million parameter RBM fails at despite achieving the same accuracy. Our hybrid computer takes a measured 50 to 64 billion probabilistic flips per second, which is at least an order of magnitude faster than superficially similar Graphics and Tensor Processing Unit (GPU/TPU) based implementations. The massively parallel architecture can comfortably perform the contrastive divergence algorithm (CD-n) with up to n = 10 million sweeps per update, beyond the capabilities of existing software implementations. These results demonstrate the potential of using Ising machines for traditionally hard-to-train deep generative Boltzmann networks, with further possible improvement in nanodevice-based realizations.

Physics-inspired Ising Computing with Ring Oscillator Activated p-bits

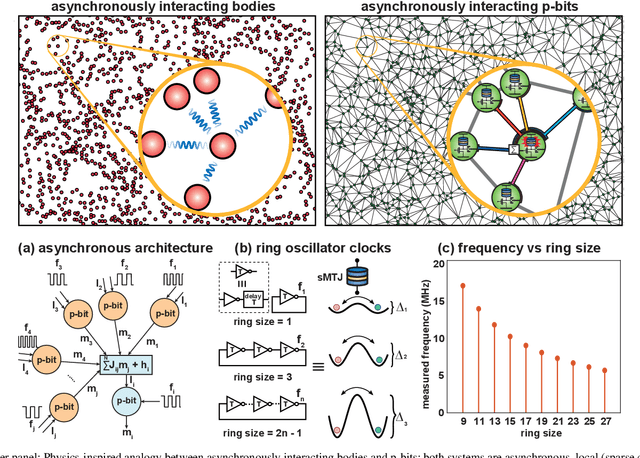
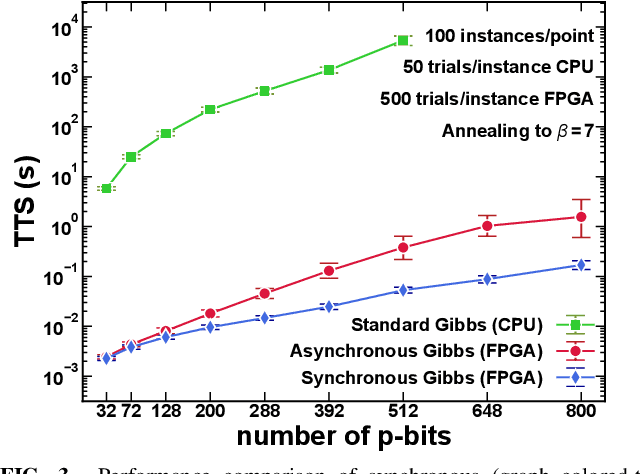
The nearing end of Moore's Law has been driving the development of domain-specific hardware tailored to solve a special set of problems. Along these lines, probabilistic computing with inherently stochastic building blocks (p-bits) have shown significant promise, particularly in the context of hard optimization and statistical sampling problems. p-bits have been proposed and demonstrated in different hardware substrates ranging from small-scale stochastic magnetic tunnel junctions (sMTJs) in asynchronous architectures to large-scale CMOS in synchronous architectures. Here, we design and implement a truly asynchronous and medium-scale p-computer (with $\approx$ 800 p-bits) that closely emulates the asynchronous dynamics of sMTJs in Field Programmable Gate Arrays (FPGAs). Using hard instances of the planted Ising glass problem on the Chimera lattice, we evaluate the performance of the asynchronous architecture against an ideal, synchronous design that performs parallelized (chromatic) exact Gibbs sampling. We find that despite the lack of any careful synchronization, the asynchronous design achieves parallelism with comparable algorithmic scaling in the ideal, carefully tuned and parallelized synchronous design. Our results highlight the promise of massively scaled p-computers with millions of free-running p-bits made out of nanoscale building blocks such as stochastic magnetic tunnel junctions.

Composable Probabilistic Inference Networks Using MRAM-based Stochastic Neurons

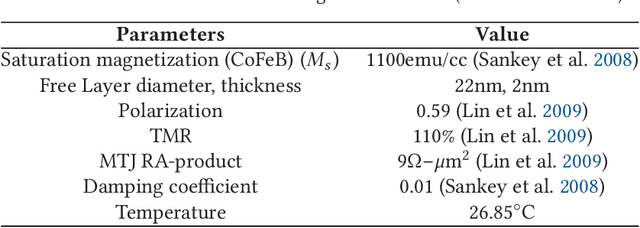
Magnetoresistive random access memory (MRAM) technologies with thermally unstable nanomagnets are leveraged to develop an intrinsic stochastic neuron as a building block for restricted Boltzmann machines (RBMs) to form deep belief networks (DBNs). The embedded MRAM-based neuron is modeled using precise physics equations. The simulation results exhibit the desired sigmoidal relation between the input voltages and probability of the output state. A probabilistic inference network simulator (PIN-Sim) is developed to realize a circuit-level model of an RBM utilizing resistive crossbar arrays along with differential amplifiers to implement the positive and negative weight values. The PIN-Sim is composed of five main blocks to train a DBN, evaluate its accuracy, and measure its power consumption. The MNIST dataset is leveraged to investigate the energy and accuracy tradeoffs of seven distinct network topologies in SPICE using the 14nm HP-FinFET technology library with the nominal voltage of 0.8V, in which an MRAM-based neuron is used as the activation function. The software and hardware level simulations indicate that a $784\times200\times10$ topology can achieve less than 5% error rates with $\sim400 pJ$ energy consumption. The error rates can be reduced to 2.5% by using a $784\times500\times500\times500\times10$ DBN at the cost of $\sim10\times$ higher energy consumption and significant area overhead. Finally, the effects of specific hardware-level parameters on power dissipation and accuracy tradeoffs are identified via the developed PIN-Sim framework.

Reservoir Computing using Stochastic p-Bits

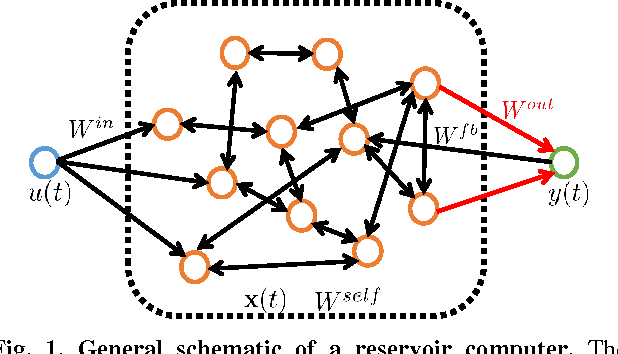
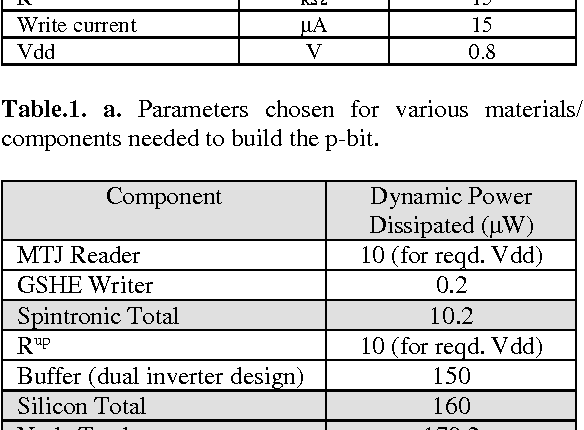
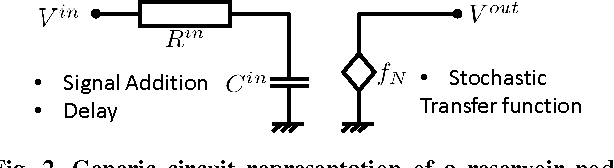
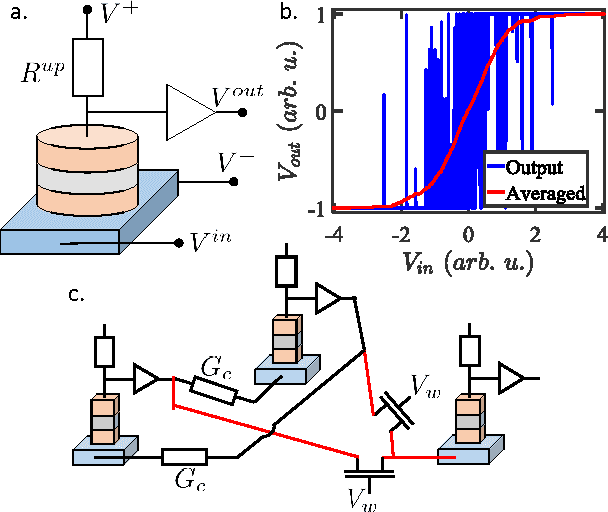
We present a general hardware framework for building networks that directly implement Reservoir Computing, a popular software method for implementing and training Recurrent Neural Networks and are particularly suited for temporal inferencing and pattern recognition. We provide a specific example of a candidate hardware unit based on a combination of soft-magnets, spin-orbit materials and CMOS transistors that can implement these networks. Efficient non von-Neumann hardware implementation of reservoir computers can open up a pathway for integration of temporal Neural Networks in a wide variety of emerging systems such as Internet of Things (IoTs), industrial controls, bio- and photo-sensors, and self-driving automotives.