Acceleration of stochastic gradient descent with momentum by averaging: finite-sample rates and asymptotic normality

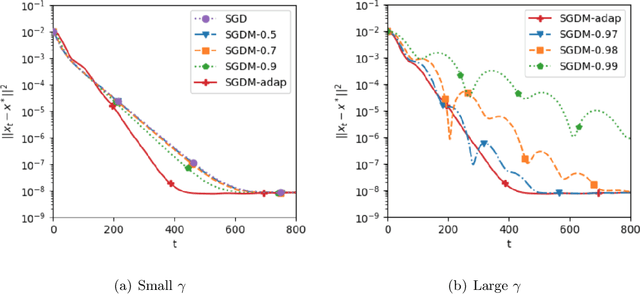
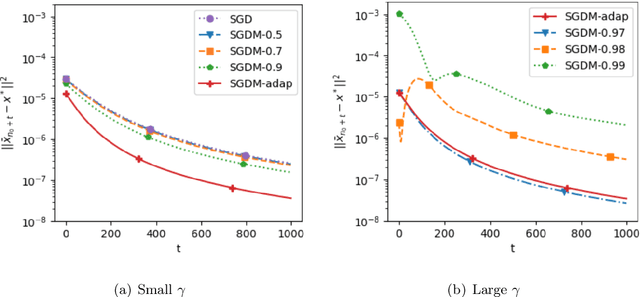
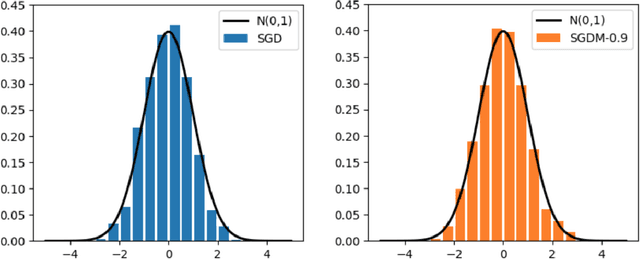
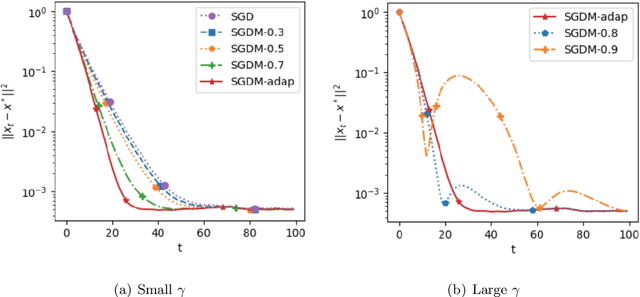
Stochastic gradient descent with momentum (SGDM) has been widely used in many machine learning and statistical applications. Despite the observed empirical benefits of SGDM over traditional SGD, the theoretical understanding of the role of momentum for different learning rates in the optimization process remains widely open. We analyze the finite-sample convergence rate of SGDM under the strongly convex settings and show that, with a large batch size, the mini-batch SGDM converges faster than mini-batch SGD to a neighborhood of the optimal value. Furthermore, we analyze the Polyak-averaging version of the SGDM estimator, establish its asymptotic normality, and justify its asymptotic equivalence to the averaged SGD.

Online Influence Maximization under Linear Threshold Model

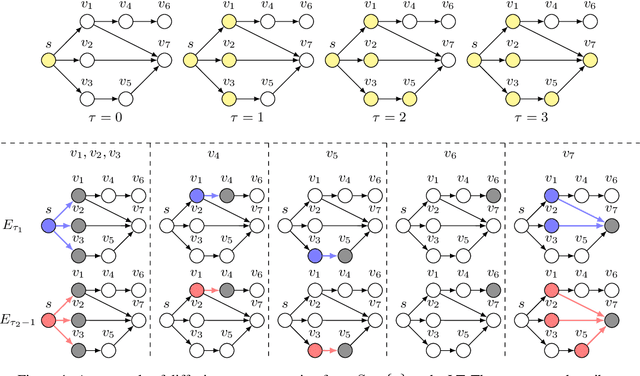
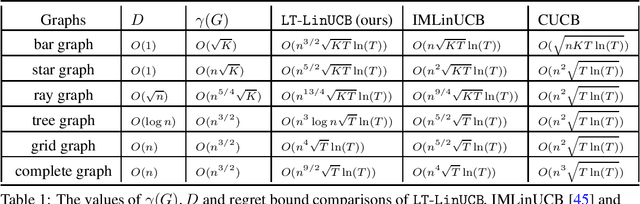
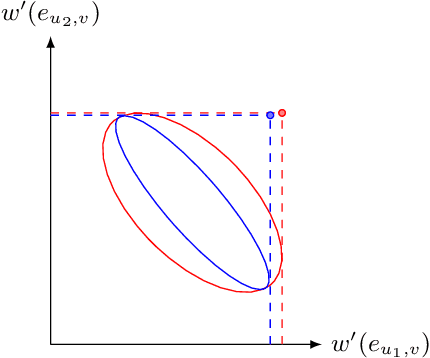
Online influence maximization (OIM) is a popular problem in social networks to learn influence propagation model parameters and maximize the influence spread at the same time. Most previous studies focus on the independent cascade (IC) model under the edge-level feedback. In this paper, we address OIM in the linear threshold (LT) model. Because node activations in the LT model are due to the aggregated effect of all active neighbors, it is more natural to model OIM with the node-level feedback. And this brings new challenge in online learning since we only observe aggregated effect from groups of nodes and the groups are also random. Based on the linear structure in node activations, we incorporate ideas from linear bandits and design an algorithm LT-LinUCB that is consistent with the observed feedback. By proving group observation modulated (GOM) bounded smoothness property, a novel result of the influence difference in terms of the random observations, we provide a regret of order $\tilde{O}(\mathrm{poly}(m)\sqrt{T})$, where $m$ is the number of edges and $T$ is the number of rounds. This is the first theoretical result in such order for OIM under the LT model. In the end, we also provide an algorithm OIM-ETC with regret bound $O(\mathrm{poly}(m)\ T^{2/3})$, which is model-independent, simple and has less requirement on online feedback and offline computation.