Model Bridging: To Interpretable Simulation Model From Neural Network

The interpretability of machine learning, particularly for deep neural networks, is strongly required when performing decision-making in a real-world application. There are several studies that show that interpretability is obtained by replacing a non-explainable neural network with an explainable simplified surrogate model. Meanwhile, another approach to understanding the target system is simulation modeled by human knowledge with interpretable simulation parameters. Recently developed simulation learning based on applications of kernel mean embedding is a method used to estimate simulation parameters as posterior distributions. However, there was no relation between the machine learning model and the simulation model. Furthermore, the computational cost of simulation learning is very expensive because of the complexity of the simulation model. To address these difficulties, we propose a ``model bridging'' framework to bridge machine learning models with simulation models by a series of kernel mean embeddings. The proposed framework enables us to obtain predictions and interpretable simulation parameters simultaneously without the computationally expensive calculations associated with simulations. In this study, we investigate a Bayesian neural network model with a few hidden layers serving as an un-explainable machine learning model. We apply the proposed framework to production simulation, which is important in the manufacturing industry.

Intractable Likelihood Regression for Covariate Shift by Kernel Mean Embedding

Simulation plays an essential role in comprehending a target system in many fields of social and industrial sciences. A major task in simulation is the estimation of parameters, and optimal parameters to express the observed data need to directly elucidate the properties of the target system as the design of the simulator is based on the expert's domain knowledge. However, skilled human experts struggle to find the desired parameters.Data assimilation therefore becomes an unavoidable task in simulator design to reduce the cost of simulator optimization. Another necessary task is extrapolation; in many practical cases, the prediction based on simulation results will be often outside of the dominant range of the given data area, and this is referred to as the covariate shift. This paper focuses on the regression problem with the covariate shift. While the parameter estimation for the covariate shift has been studied thoroughly in parametric and nonparametric settings, conventional statistical methods of parameter searching are not applicable in the data assimilation of the simulation owing to the properties of the likelihood function: intractable or nondifferentiable. To address these problems, we propose a novel framework of Bayesian inference based on kernel mean embedding that comprises an extended kernel approximate Bayesian computation (ABC) of the importance weighted regression, kernel herding, and the kernel sum rule. This framework makes the prediction available in covariate shift situations, and its effectiveness is evaluated in both synthetic numerical experiments and a widely used production simulator.

Kernel Recursive ABC: Point Estimation with Intractable Likelihood

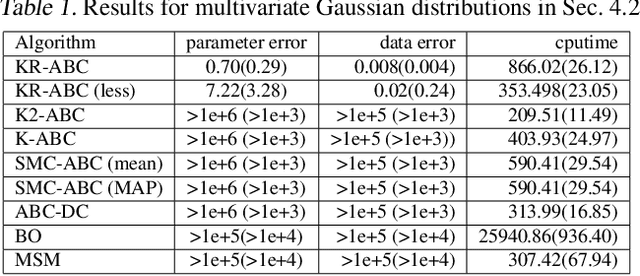
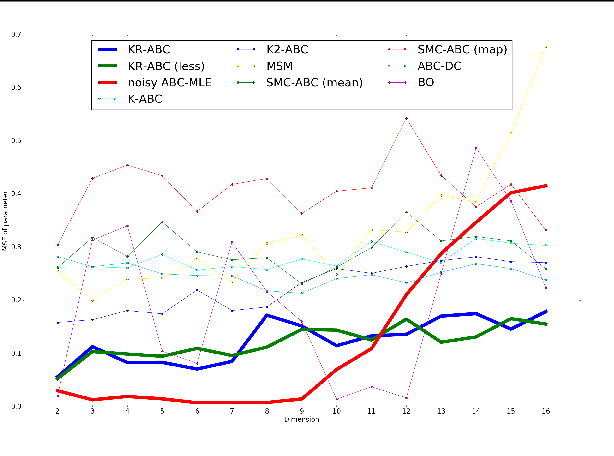
We propose a novel approach to parameter estimation for simulator-based statistical models with intractable likelihood. Our proposed method involves recursive application of kernel ABC and kernel herding to the same observed data. We provide a theoretical explanation regarding why the approach works, showing (for the population setting) that, under a certain assumption, point estimates obtained with this method converge to the true parameter, as recursion proceeds. We have conducted a variety of numerical experiments, including parameter estimation for a real-world pedestrian flow simulator, and show that in most cases our method outperforms existing approaches.

Bayesian Estimation of Multidimensional Latent Variables and Its Asymptotic Accuracy

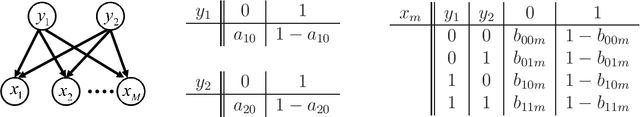
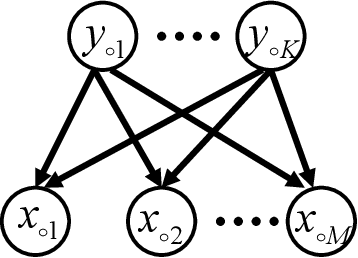
Hierarchical learning models, such as mixture models and Bayesian networks, are widely employed for unsupervised learning tasks, such as clustering analysis. They consist of observable and hidden variables, which represent the given data and their hidden generation process, respectively. It has been pointed out that conventional statistical analysis is not applicable to these models, because redundancy of the latent variable produces singularities in the parameter space. In recent years, a method based on algebraic geometry has allowed us to analyze the accuracy of predicting observable variables when using Bayesian estimation. However, how to analyze latent variables has not been sufficiently studied, even though one of the main issues in unsupervised learning is to determine how accurately the latent variable is estimated. A previous study proposed a method that can be used when the range of the latent variable is redundant compared with the model generating data. The present paper extends that method to the situation in which the latent variables have redundant dimensions. We formulate new error functions and derive their asymptotic forms. Calculation of the error functions is demonstrated in two-layered Bayesian networks.

Effects of Additional Data on Bayesian Clustering

Hierarchical probabilistic models, such as mixture models, are used for cluster analysis. These models have two types of variables: observable and latent. In cluster analysis, the latent variable is estimated, and it is expected that additional information will improve the accuracy of the estimation of the latent variable. Many proposed learning methods are able to use additional data; these include semi-supervised learning and transfer learning. However, from a statistical point of view, a complex probabilistic model that encompasses both the initial and additional data might be less accurate due to having a higher-dimensional parameter. The present paper presents a theoretical analysis of the accuracy of such a model and clarifies which factor has the greatest effect on its accuracy, the advantages of obtaining additional data, and the disadvantages of increasing the complexity.

Asymptotic Accuracy of Bayesian Estimation for a Single Latent Variable

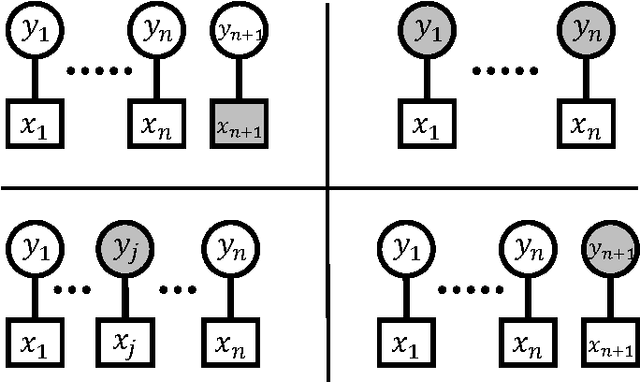
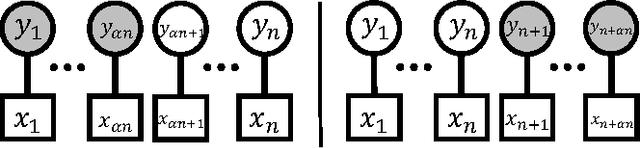
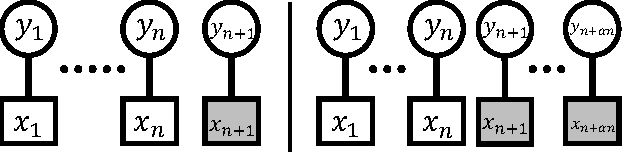
In data science and machine learning, hierarchical parametric models, such as mixture models, are often used. They contain two kinds of variables: observable variables, which represent the parts of the data that can be directly measured, and latent variables, which represent the underlying processes that generate the data. Although there has been an increase in research on the estimation accuracy for observable variables, the theoretical analysis of estimating latent variables has not been thoroughly investigated. In a previous study, we determined the accuracy of a Bayes estimation for the joint probability of the latent variables in a dataset, and we proved that the Bayes method is asymptotically more accurate than the maximum-likelihood method. However, the accuracy of the Bayes estimation for a single latent variable remains unknown. In the present paper, we derive the asymptotic expansions of the error functions, which are defined by the Kullback-Leibler divergence, for two types of single-variable estimations when the statistical regularity is satisfied. Our results indicate that the accuracies of the Bayes and maximum-likelihood methods are asymptotically equivalent and clarify that the Bayes method is only advantageous for multivariable estimations.

Accuracy of Latent-Variable Estimation in Bayesian Semi-Supervised Learning

Hierarchical probabilistic models, such as Gaussian mixture models, are widely used for unsupervised learning tasks. These models consist of observable and latent variables, which represent the observable data and the underlying data-generation process, respectively. Unsupervised learning tasks, such as cluster analysis, are regarded as estimations of latent variables based on the observable ones. The estimation of latent variables in semi-supervised learning, where some labels are observed, will be more precise than that in unsupervised, and one of the concerns is to clarify the effect of the labeled data. However, there has not been sufficient theoretical analysis of the accuracy of the estimation of latent variables. In a previous study, a distribution-based error function was formulated, and its asymptotic form was calculated for unsupervised learning with generative models. It has been shown that, for the estimation of latent variables, the Bayes method is more accurate than the maximum-likelihood method. The present paper reveals the asymptotic forms of the error function in Bayesian semi-supervised learning for both discriminative and generative models. The results show that the generative model, which uses all of the given data, performs better when the model is well specified.

Asymptotic Accuracy of Distribution-Based Estimation for Latent Variables

Hierarchical statistical models are widely employed in information science and data engineering. The models consist of two types of variables: observable variables that represent the given data and latent variables for the unobservable labels. An asymptotic analysis of the models plays an important role in evaluating the learning process; the result of the analysis is applied not only to theoretical but also to practical situations, such as optimal model selection and active learning. There are many studies of generalization errors, which measure the prediction accuracy of the observable variables. However, the accuracy of estimating the latent variables has not yet been elucidated. For a quantitative evaluation of this, the present paper formulates distribution-based functions for the errors in the estimation of the latent variables. The asymptotic behavior is analyzed for both the maximum likelihood and the Bayes methods.

Asymptotic Accuracy of Bayes Estimation for Latent Variables with Redundancy

Hierarchical parametric models consisting of observable and latent variables are widely used for unsupervised learning tasks. For example, a mixture model is a representative hierarchical model for clustering. From the statistical point of view, the models can be regular or singular due to the distribution of data. In the regular case, the models have the identifiability; there is one-to-one relation between a probability density function for the model expression and the parameter. The Fisher information matrix is positive definite, and the estimation accuracy of both observable and latent variables has been studied. In the singular case, on the other hand, the models are not identifiable and the Fisher matrix is not positive definite. Conventional statistical analysis based on the inverse Fisher matrix is not applicable. Recently, an algebraic geometrical analysis has been developed and is used to elucidate the Bayes estimation of observable variables. The present paper applies this analysis to latent-variable estimation and determines its theoretical performance. Our results clarify behavior of the convergence of the posterior distribution. It is found that the posterior of the observable-variable estimation can be different from the one in the latent-variable estimation. Because of the difference, the Markov chain Monte Carlo method based on the parameter and the latent variable cannot construct the desired posterior distribution.

Stochastic complexity of Bayesian networks

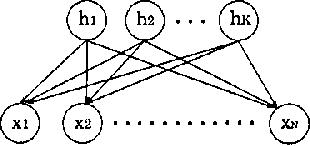
Bayesian networks are now being used in enormous fields, for example, diagnosis of a system, data mining, clustering and so on. In spite of their wide range of applications, the statistical properties have not yet been clarified, because the models are nonidentifiable and non-regular. In a Bayesian network, the set of its parameter for a smaller model is an analytic set with singularities in the space of large ones. Because of these singularities, the Fisher information matrices are not positive definite. In other words, the mathematical foundation for learning was not constructed. In recent years, however, we have developed a method to analyze non-regular models using algebraic geometry. This method revealed the relation between the models singularities and its statistical properties. In this paper, applying this method to Bayesian networks with latent variables, we clarify the order of the stochastic complexities.Our result claims that the upper bound of those is smaller than the dimension of the parameter space. This means that the Bayesian generalization error is also far smaller than that of regular model, and that Schwarzs model selection criterion BIC needs to be improved for Bayesian networks.