Sumio Watanbe
Stochastic complexity of Bayesian networks
Oct 19, 2012
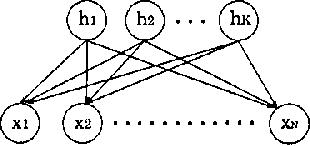
Abstract:Bayesian networks are now being used in enormous fields, for example, diagnosis of a system, data mining, clustering and so on. In spite of their wide range of applications, the statistical properties have not yet been clarified, because the models are nonidentifiable and non-regular. In a Bayesian network, the set of its parameter for a smaller model is an analytic set with singularities in the space of large ones. Because of these singularities, the Fisher information matrices are not positive definite. In other words, the mathematical foundation for learning was not constructed. In recent years, however, we have developed a method to analyze non-regular models using algebraic geometry. This method revealed the relation between the models singularities and its statistical properties. In this paper, applying this method to Bayesian networks with latent variables, we clarify the order of the stochastic complexities.Our result claims that the upper bound of those is smaller than the dimension of the parameter space. This means that the Bayesian generalization error is also far smaller than that of regular model, and that Schwarzs model selection criterion BIC needs to be improved for Bayesian networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge