Asymptotic Accuracy of Bayesian Estimation for a Single Latent Variable
Paper and Code
Apr 17, 2015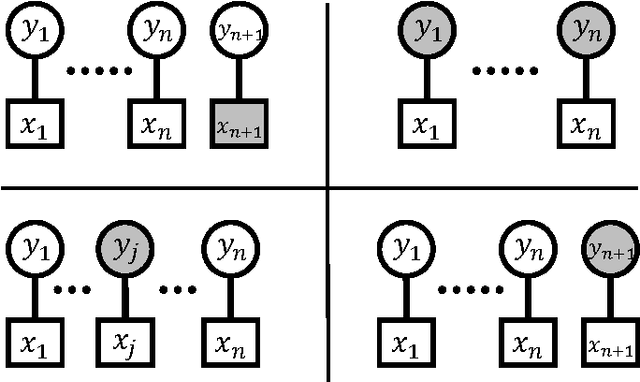

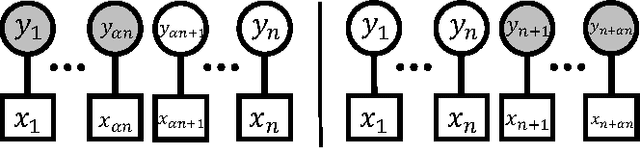
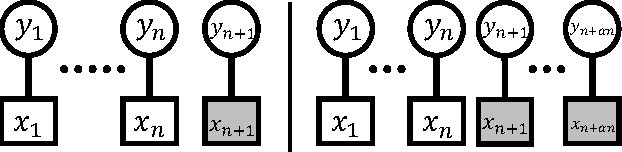
In data science and machine learning, hierarchical parametric models, such as mixture models, are often used. They contain two kinds of variables: observable variables, which represent the parts of the data that can be directly measured, and latent variables, which represent the underlying processes that generate the data. Although there has been an increase in research on the estimation accuracy for observable variables, the theoretical analysis of estimating latent variables has not been thoroughly investigated. In a previous study, we determined the accuracy of a Bayes estimation for the joint probability of the latent variables in a dataset, and we proved that the Bayes method is asymptotically more accurate than the maximum-likelihood method. However, the accuracy of the Bayes estimation for a single latent variable remains unknown. In the present paper, we derive the asymptotic expansions of the error functions, which are defined by the Kullback-Leibler divergence, for two types of single-variable estimations when the statistical regularity is satisfied. Our results indicate that the accuracies of the Bayes and maximum-likelihood methods are asymptotically equivalent and clarify that the Bayes method is only advantageous for multivariable estimations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge