X-ray dark-field via spectral propagation-based imaging

Dark-field X-ray imaging is a novel modality which visualises scattering from unresolved microstructure. Current dark-field imaging techniques typically require precision optics in a stable environment. Propagation-based imaging (PBI) is an optics-free phase-contrast imaging technique that can be used to recover phase information by modelling the propagation of a diffracted wavefield. Based on the Fokker--Planck equation of X-ray imaging, we propose a dual-energy PBI approach to capture phase and dark-field effects. The equation is solved under conditions of a single-material sample with spatially slowly-varying dark-field signal, together with an a priori dark-field spectral dependence. We use single-grid dark-field imaging to fit a power law to the dark-field spectral dependence, and successfully apply the PBI dark-field retrieval algorithm to simulated and experimental dual-energy data.

Paraxial diffusion-field retrieval

Unresolved spatially-random microstructure, in an illuminated sample, can lead to position-dependent blur when an image of that sample is taken using an incoherent imaging system. For a small propagation distance, between the exit surface of the sample and the entrance surface of a position-sensitive detector, the paraxial approximation implies that the blurring influence of the sample may be modeled using an anomalous-diffusion field. This diffusion field may have a scalar or tensor character, depending on whether the random microstructure has an autocorrelation function that is rotationally isotropic or anisotropic, respectively. Partial differential equations are written down and then solved, in a closed-form manner, for several variants of the inverse problem of diffusion-field retrieval given suitable intensity images. Both uniform-illumination and structured-illumination schemes are considered. Links are made, between the recovered diffusion field and certain statistical properties of the unresolved microstructure. The developed theory -- which may be viewed as a crudely parallel form of small-angle scattering under the Guinier approximation -- is applicable to a range of paraxial radiation and matter fields, such as visible light, x rays, neutrons, and electrons.

Tomographic phase and attenuation extraction for a sample composed of unknown materials using X-ray propagation-based phase-contrast imaging

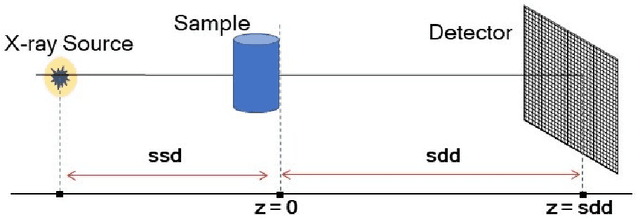
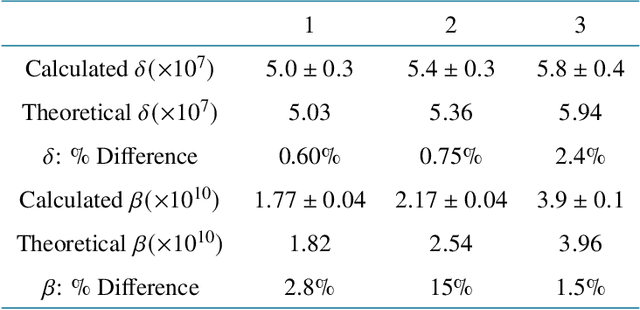
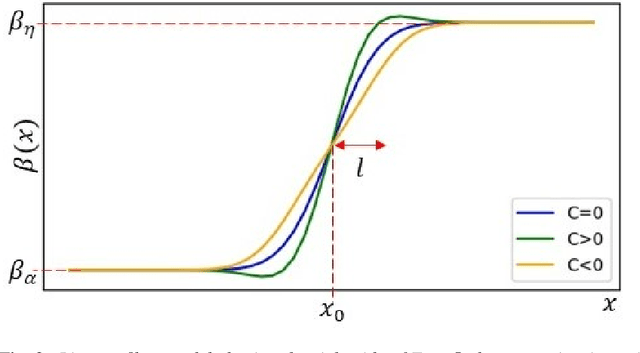
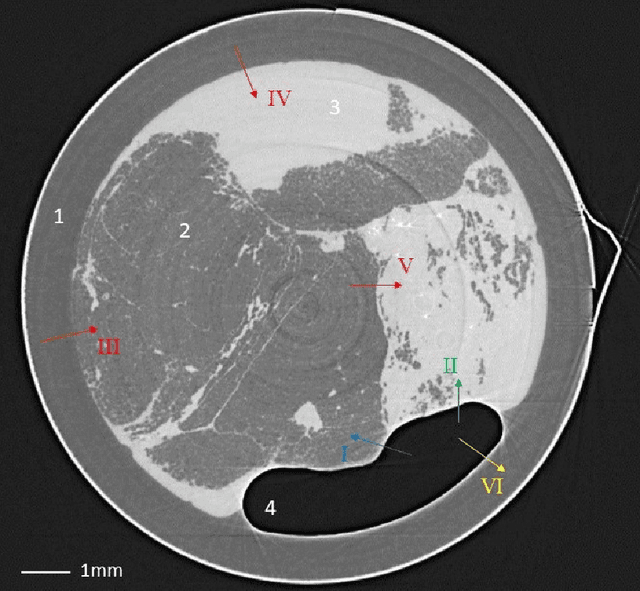
Propagation-based phase-contrast X-ray imaging (PB-PCXI) generates image contrast by utilizing sample-imposed phase-shifts. This has proven useful when imaging weakly-attenuating samples, as conventional attenuation-based imaging does not always provide adequate contrast. We present a PB-PCXI algorithm capable of extracting the X-ray attenuation, $\beta$, and refraction, $\delta$, components of the complex refractive index of distinct materials within an unknown sample. The method involves curve-fitting an error-function-based model to a phase-retrieved interface in a PB-PCXI tomographic reconstruction, which is obtained when Paganin-type phase-retrieval is applied with incorrect values of $\delta$ and $\beta$. The fit parameters can then be used to calculate true $\delta$ and $\beta$ values for composite materials. This approach requires no a priori sample information, making it broadly applicable. Our PB-PCXI reconstruction is single distance, requiring only one exposure per tomographic angle, which is important for radiosensitive samples. We apply this approach to a breast-tissue sample, recovering the refraction component, $\delta$, with 0.6 - 2.4\% accuracy compared to theoretical values.