X-ray dark-field via spectral propagation-based imaging

Dark-field X-ray imaging is a novel modality which visualises scattering from unresolved microstructure. Current dark-field imaging techniques typically require precision optics in a stable environment. Propagation-based imaging (PBI) is an optics-free phase-contrast imaging technique that can be used to recover phase information by modelling the propagation of a diffracted wavefield. Based on the Fokker--Planck equation of X-ray imaging, we propose a dual-energy PBI approach to capture phase and dark-field effects. The equation is solved under conditions of a single-material sample with spatially slowly-varying dark-field signal, together with an a priori dark-field spectral dependence. We use single-grid dark-field imaging to fit a power law to the dark-field spectral dependence, and successfully apply the PBI dark-field retrieval algorithm to simulated and experimental dual-energy data.

Tomographic phase and attenuation extraction for a sample composed of unknown materials using X-ray propagation-based phase-contrast imaging

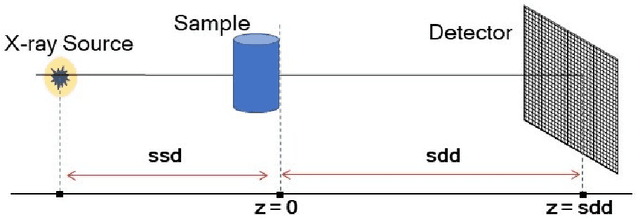
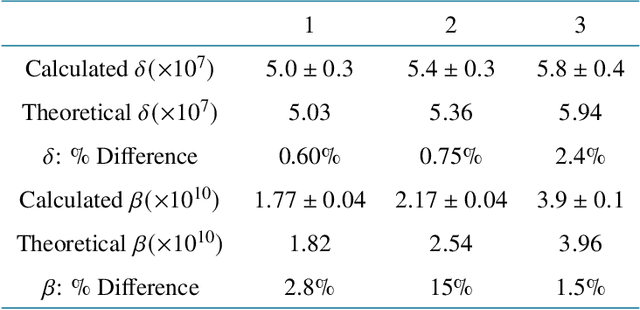
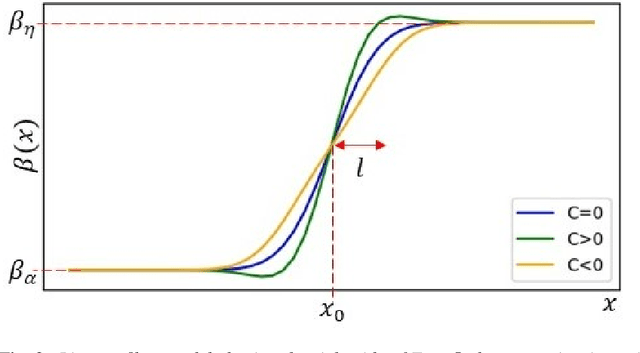
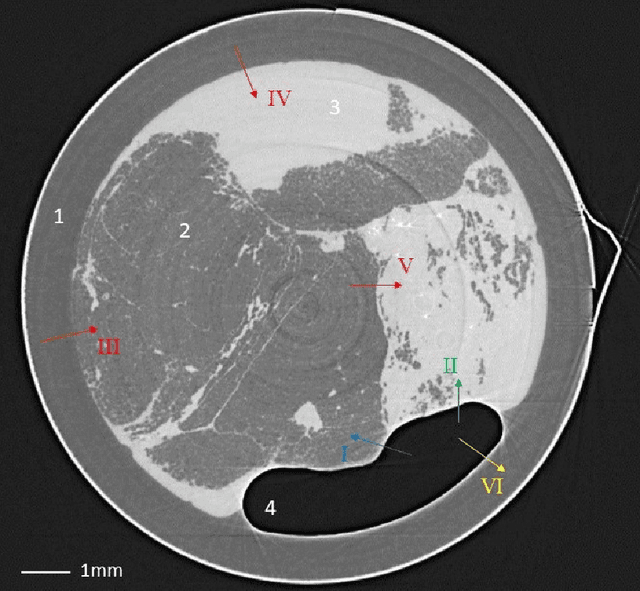
Propagation-based phase-contrast X-ray imaging (PB-PCXI) generates image contrast by utilizing sample-imposed phase-shifts. This has proven useful when imaging weakly-attenuating samples, as conventional attenuation-based imaging does not always provide adequate contrast. We present a PB-PCXI algorithm capable of extracting the X-ray attenuation, $\beta$, and refraction, $\delta$, components of the complex refractive index of distinct materials within an unknown sample. The method involves curve-fitting an error-function-based model to a phase-retrieved interface in a PB-PCXI tomographic reconstruction, which is obtained when Paganin-type phase-retrieval is applied with incorrect values of $\delta$ and $\beta$. The fit parameters can then be used to calculate true $\delta$ and $\beta$ values for composite materials. This approach requires no a priori sample information, making it broadly applicable. Our PB-PCXI reconstruction is single distance, requiring only one exposure per tomographic angle, which is important for radiosensitive samples. We apply this approach to a breast-tissue sample, recovering the refraction component, $\delta$, with 0.6 - 2.4\% accuracy compared to theoretical values.