Kaveh Dehghanpour
Mitigating Smart Meter Asynchrony Error Via Multi-Objective Low Rank Matrix Recovery
May 11, 2021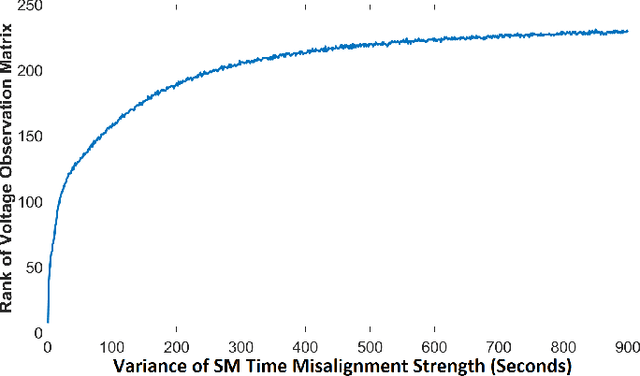
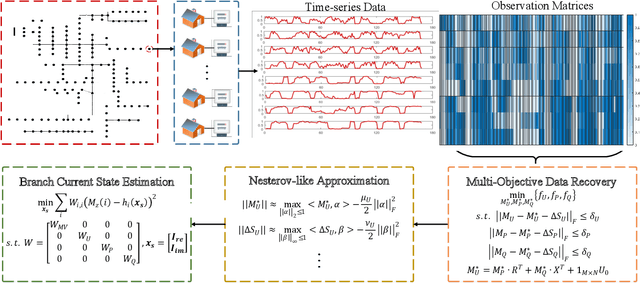
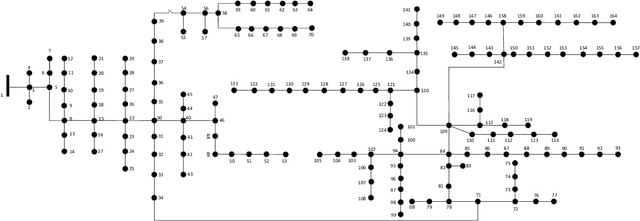
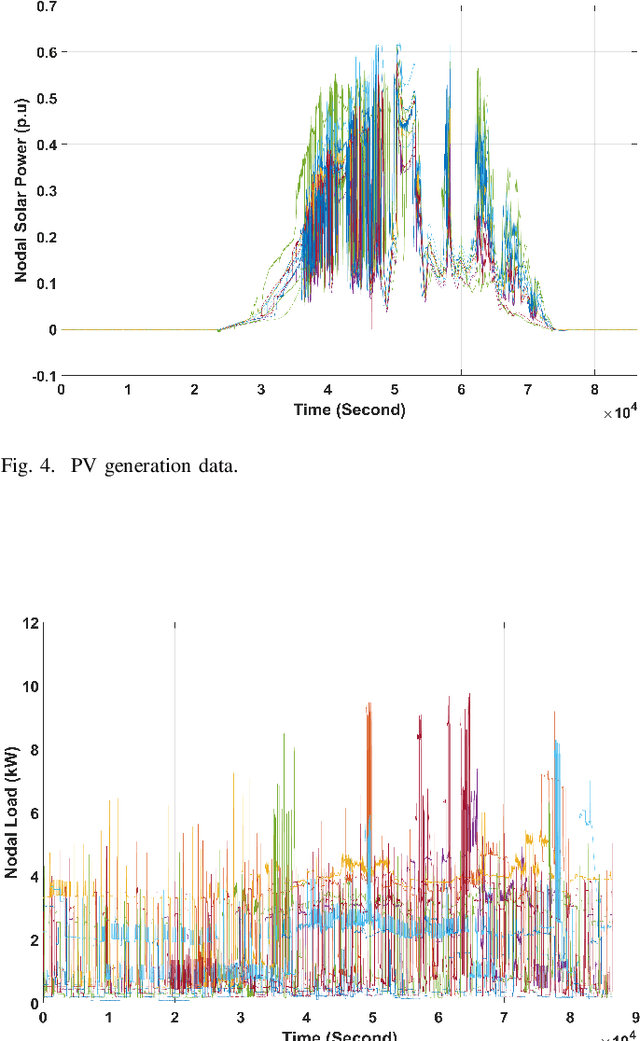
Abstract:Smart meters (SMs) are being widely deployed by distribution utilities across the U.S. Despite their benefits in real-time monitoring. SMs suffer from certain data quality issues; specifically, unlike phasor measurement units (PMUs) that use GPS for data synchronization, SMs are not perfectly synchronized. The asynchrony error can degrade the monitoring accuracy in distribution networks. To address this challenge, we propose a principal component pursuit (PCP)-based data recovery strategy. Since asynchrony results in a loss of temporal correlation among SMs, the key idea in our solution is to leverage a PCP-based low rank matrix recovery technique to maximize the temporal correlation between multiple data streams obtained from SMs. Further, our approach has a novel multi-objective structure, which allows utilities to precisely refine and recover all SM-measured variables, including voltage and power measurements, while incorporating their inherent dependencies through power flow equations. We have performed numerical experiments using real SM data to demonstrate the effectiveness of the proposed strategy in mitigating the impact of SM asynchrony on distribution grid monitoring.
A Hierarchical Deep Actor-Critic Learning Method for Joint Distribution System State Estimation
Dec 04, 2020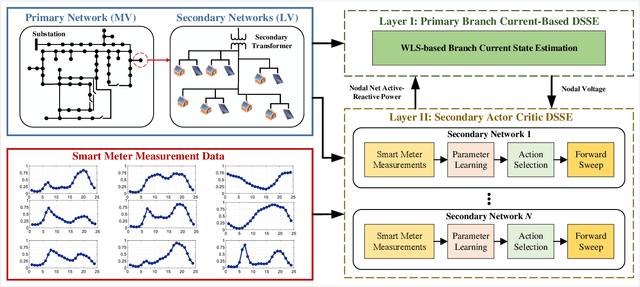
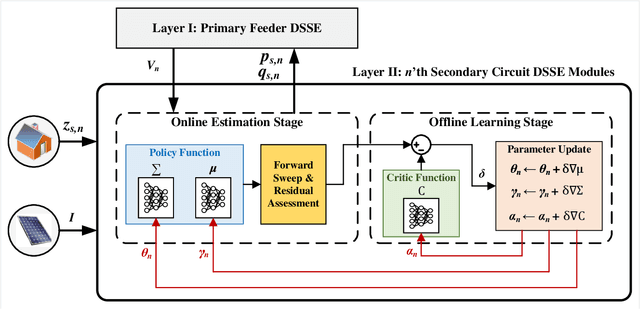
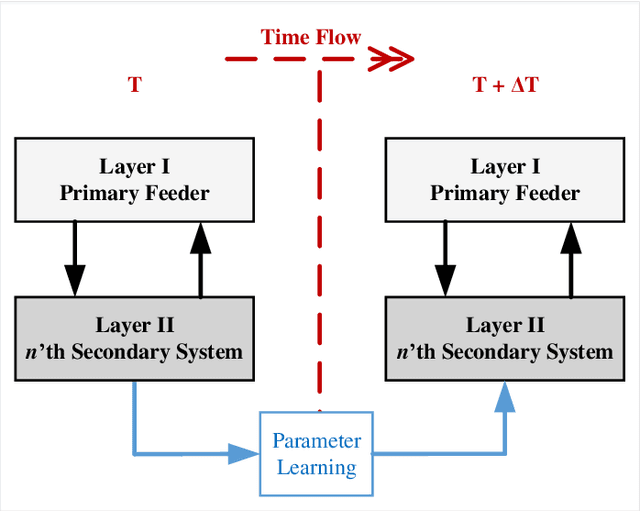
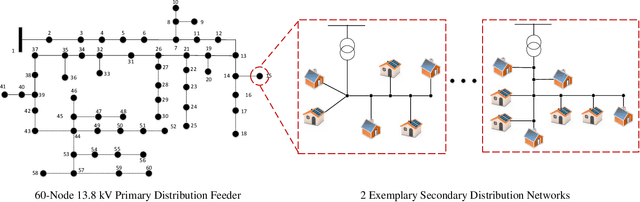
Abstract:Due to increasing penetration of volatile distributed photovoltaic (PV) resources, real-time monitoring of customers at the grid-edge has become a critical task. However, this requires solving the distribution system state estimation (DSSE) jointly for both primary and secondary levels of distribution grids, which is computationally complex and lacks scalability to large systems. To achieve near real-time solutions for DSSE, we present a novel hierarchical reinforcement learning-aided framework: at the first layer, a weighted least squares (WLS) algorithm solves the DSSE over primary medium-voltage feeders; at the second layer, deep actor-critic (A-C) modules are trained for each secondary transformer using measurement residuals to estimate the states of low-voltage circuits and capture the impact of PVs at the grid-edge. While the A-C parameter learning process takes place offline, the trained A-C modules are deployed online for fast secondary grid state estimation; this is the key factor in scalability and computational efficiency of the framework. To maintain monitoring accuracy, the two levels exchange boundary information with each other at the secondary nodes, including transformer voltages (first layer to second layer) and active/reactive total power injection (second layer to first layer). This interactive information passing strategy results in a closed-loop structure that is able to track optimal solutions at both layers in few iterations. Moreover, our model can handle the topology changes using the Jacobian matrices of the first layer. We have performed numerical experiments using real utility data and feeder models to verify the performance of the proposed framework.
Multi-Source Data-Driven Outage Location in Distribution Systems Using Probabilistic Graph Learning
Dec 04, 2020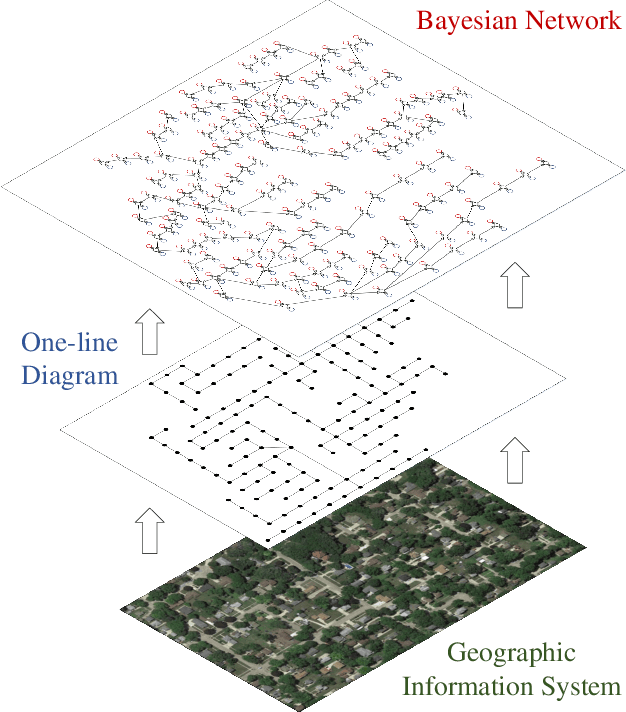
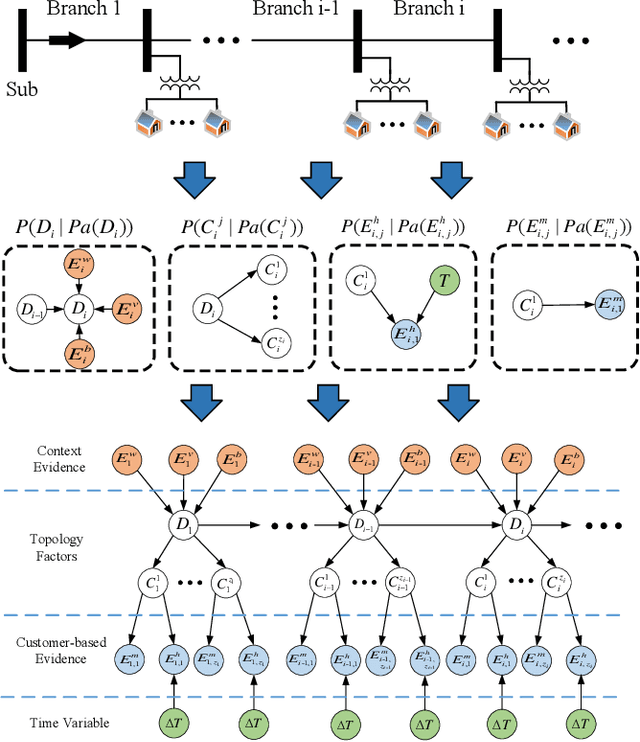
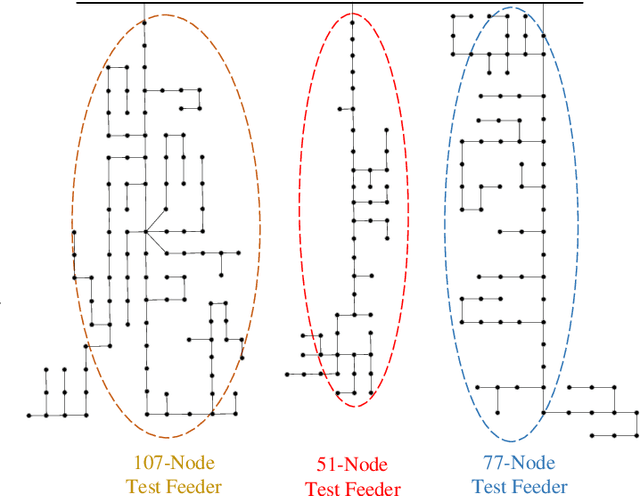
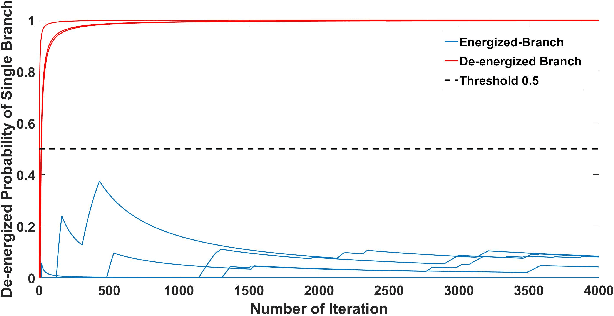
Abstract:Efficient outage location is critical to enhancing the resilience of power systems. However, accurate outage location requires combining massive evidence received from diverse data sources, including smart meter (SM) signals, customer trouble calls, social media messages, weather data, vegetation information, and physical parameters of the network. This is a computationally complex task due to the high dimensionality of data in distribution grids. In this paper, we propose a multi-source data fusion approach to locate outage events in partially observable distribution systems using Bayesian networks (BNs). A novel aspect of the proposed approach is that it takes multi-source evidence and the complex structure of distribution systems into account using a probabilistic graphical method. This method can radically reduce the computational complexity of outage location inference in high-dimensional spaces. The graphical structure of the proposed BN is established based on the grid's topology and the causal relationship between random variables, such as the states of branches/customers and evidence. Utilizing this graphical model, the locations of outages are obtained by leveraging a Gibbs sampling (GS) method, to infer the probabilities of de-energization for all branches. Compared with commonly-used exact inference methods that have exponential complexity in the size of the BN, GS quantifies the target conditional probability distributions in a timely manner. A case study of several real partially observable systems is presented to validate the method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge