Multi-Source Data-Driven Outage Location in Distribution Systems Using Probabilistic Graph Learning

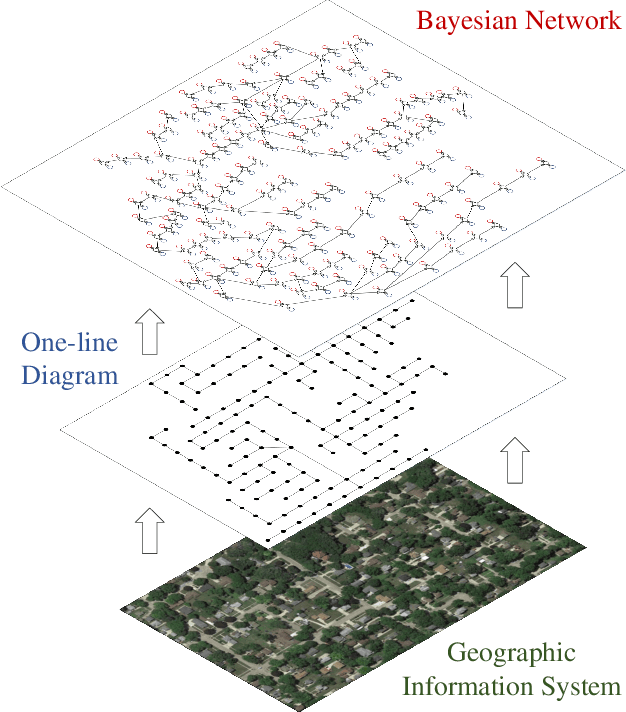
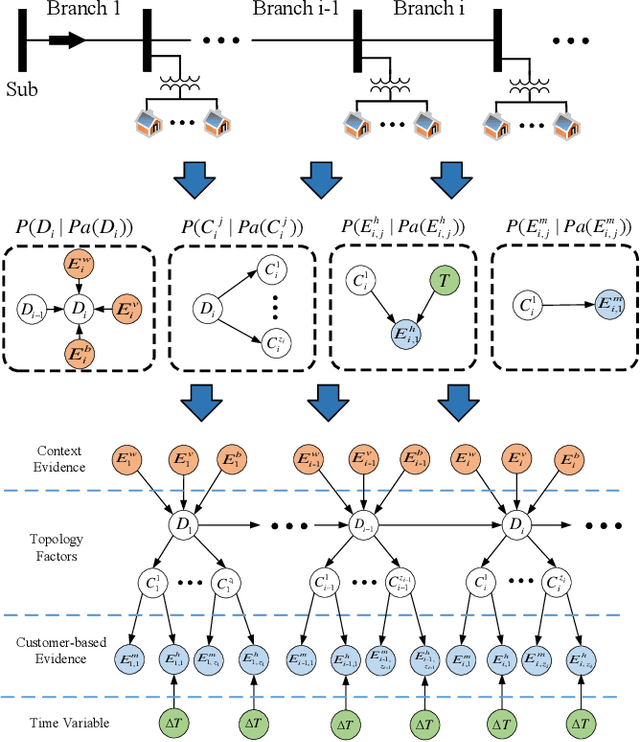
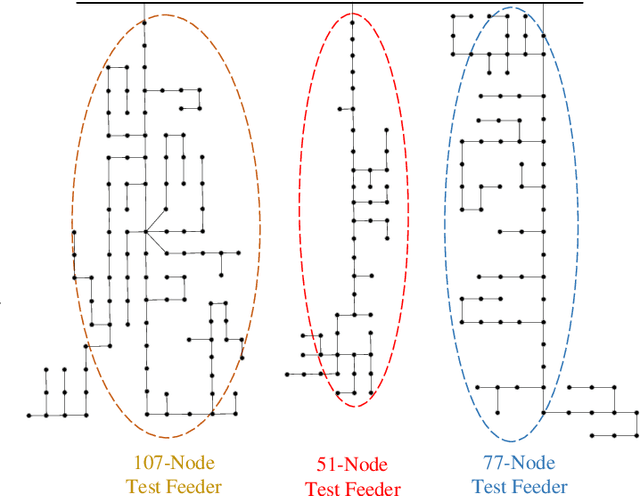
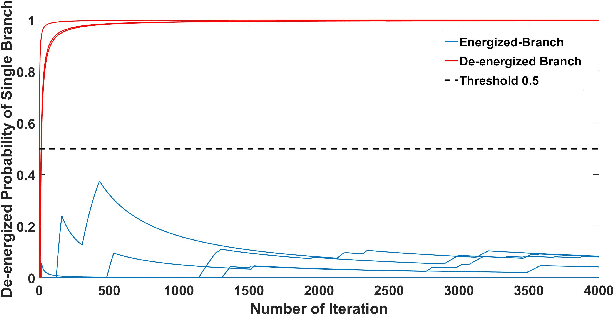
Efficient outage location is critical to enhancing the resilience of power systems. However, accurate outage location requires combining massive evidence received from diverse data sources, including smart meter (SM) signals, customer trouble calls, social media messages, weather data, vegetation information, and physical parameters of the network. This is a computationally complex task due to the high dimensionality of data in distribution grids. In this paper, we propose a multi-source data fusion approach to locate outage events in partially observable distribution systems using Bayesian networks (BNs). A novel aspect of the proposed approach is that it takes multi-source evidence and the complex structure of distribution systems into account using a probabilistic graphical method. This method can radically reduce the computational complexity of outage location inference in high-dimensional spaces. The graphical structure of the proposed BN is established based on the grid's topology and the causal relationship between random variables, such as the states of branches/customers and evidence. Utilizing this graphical model, the locations of outages are obtained by leveraging a Gibbs sampling (GS) method, to infer the probabilities of de-energization for all branches. Compared with commonly-used exact inference methods that have exponential complexity in the size of the BN, GS quantifies the target conditional probability distributions in a timely manner. A case study of several real partially observable systems is presented to validate the method.