Ironing the Graphs: Toward a Correct Geometric Analysis of Large-Scale Graphs

Graph embedding approaches attempt to project graphs into geometric entities, i.e, manifolds. The idea is that the geometric properties of the projected manifolds are helpful in the inference of graph properties. However, if the choice of the embedding manifold is incorrectly performed, it can lead to incorrect geometric inference. In this paper, we argue that the classical embedding techniques cannot lead to correct geometric interpretation as they miss the curvature at each point, of manifold. We advocate that for doing correct geometric interpretation the embedding of graph should be done over regular constant curvature manifolds. To this end, we present an embedding approach, the discrete Ricci flow graph embedding (dRfge) based on the discrete Ricci flow that adapts the distance between nodes in a graph so that the graph can be embedded onto a constant curvature manifold that is homogeneous and isotropic, i.e., all directions are equivalent and distances comparable, resulting in correct geometric interpretations. A major contribution of this paper is that for the first time, we prove the convergence of discrete Ricci flow to a constant curvature and stable distance metrics over the edges. A drawback of using the discrete Ricci flow is the high computational complexity that prevented its usage in large-scale graph analysis. Another contribution of this paper is a new algorithmic solution that makes it feasible to calculate the Ricci flow for graphs of up to 50k nodes, and beyond. The intuitions behind the discrete Ricci flow make it possible to obtain new insights into the structure of large-scale graphs. We demonstrate this through a case study on analyzing the internet connectivity structure between countries at the BGP level.

BERT4CTR: An Efficient Framework to Combine Pre-trained Language Model with Non-textual Features for CTR Prediction

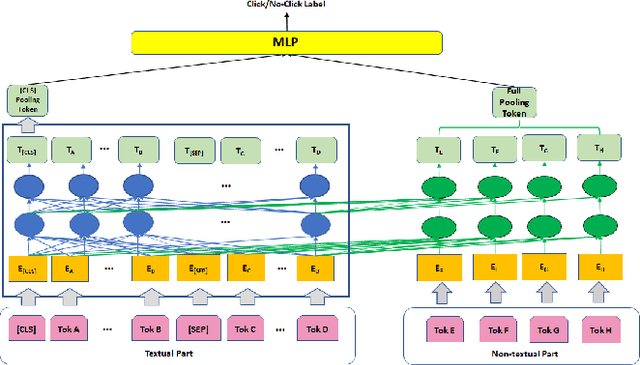
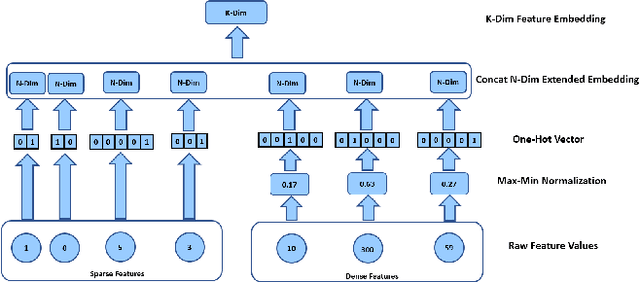
Although deep pre-trained language models have shown promising benefit in a large set of industrial scenarios, including Click-Through-Rate (CTR) prediction, how to integrate pre-trained language models that handle only textual signals into a prediction pipeline with non-textual features is challenging. Up to now two directions have been explored to integrate multi-modal inputs in fine-tuning of pre-trained language models. One consists of fusing the outcome of language models and non-textual features through an aggregation layer, resulting into ensemble framework, where the cross-information between textual and non-textual inputs are only learned in the aggregation layer. The second one consists of splitting non-textual features into fine-grained fragments and transforming the fragments to new tokens combined with textual ones, so that they can be fed directly to transformer layers in language models. However, this approach increases the complexity of the learning and inference because of the numerous additional tokens. To address these limitations, we propose in this work a novel framework BERT4CTR, with the Uni-Attention mechanism that can benefit from the interactions between non-textual and textual features while maintaining low time-costs in training and inference through a dimensionality reduction. Comprehensive experiments on both public and commercial data demonstrate that BERT4CTR can outperform significantly the state-of-the-art frameworks to handle multi-modal inputs and be applicable to CTR prediction.

A Geometric Approach for Real-time Monitoring of Dynamic Large Scale Graphs: AS-level graphs illustrated

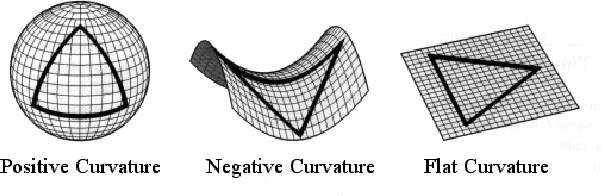
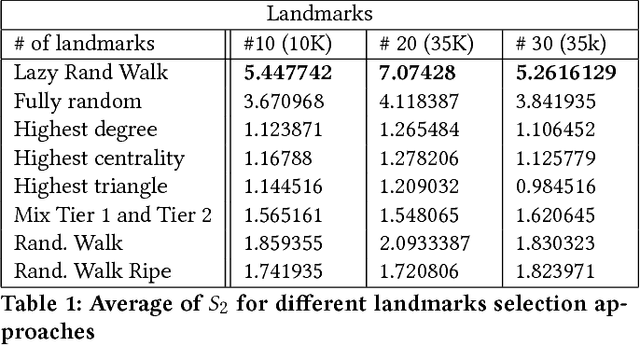
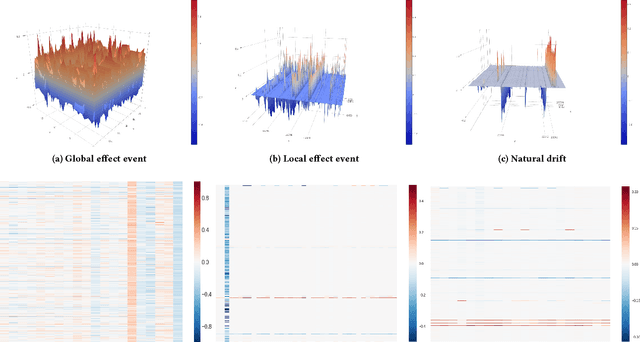
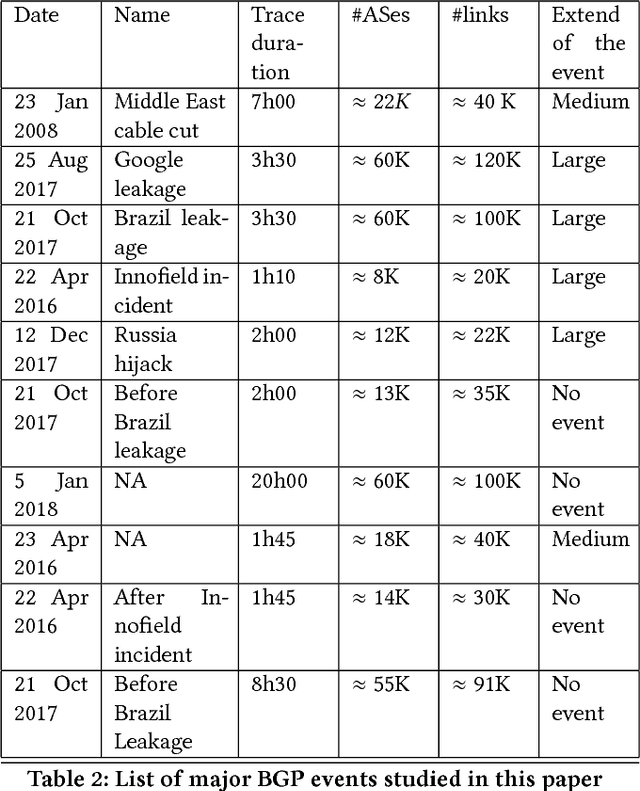
The monitoring of large dynamic networks is a major chal- lenge for a wide range of application. The complexity stems from properties of the underlying graphs, in which slight local changes can lead to sizable variations of global prop- erties, e.g., under certain conditions, a single link cut that may be overlooked during monitoring can result in splitting the graph into two disconnected components. Moreover, it is often difficult to determine whether a change will propagate globally or remain local. Traditional graph theory measure such as the centrality or the assortativity of the graph are not satisfying to characterize global properties of the graph. In this paper, we tackle the problem of real-time monitoring of dynamic large scale graphs by developing a geometric approach that leverages notions of geometric curvature and recent development in graph embeddings using Ollivier-Ricci curvature [47]. We illustrate the use of our method by consid- ering the practical case of monitoring dynamic variations of global Internet using topology changes information provided by combining several BGP feeds. In particular, we use our method to detect major events and changes via the geometry of the embedding of the graph.