Towards Robust Monocular Depth Estimation: Mixing Datasets for Zero-Shot Cross-Dataset Transfer

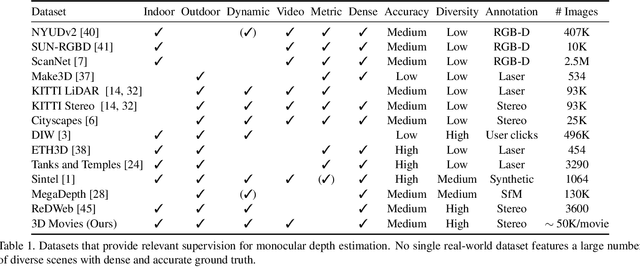
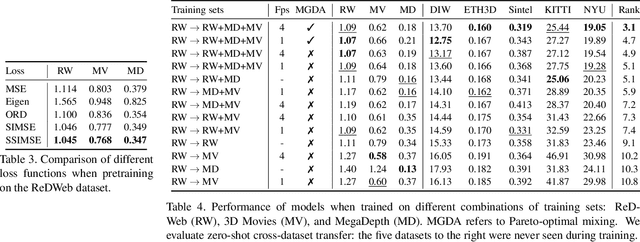
The success of monocular depth estimation relies on large and diverse training sets. Due to the challenges associated with acquiring dense ground-truth depth across different environments at scale, a number of datasets with distinct characteristics and biases have emerged. We develop tools that enable mixing multiple datasets during training, even if their annotations are incompatible. In particular, we propose a training objective that is invariant to changes in depth range and scale. Armed with this objective, we explore an abundant source of training data: 3D films. We demonstrate that despite pervasive inaccuracies, 3D films constitute a useful source of data that is complementary to existing training sets. We evaluate the presented approach on diverse datasets, focusing on zero-shot cross-dataset transfer: testing the generality of the learned model by evaluating it on datasets that were not seen during training. The experiments confirm that mixing data from complementary sources yields improved depth estimates, particularly on previously unseen datasets. Some results are shown in the supplementary video: https://youtu.be/ITI0YS6IrUQ

3D Fluid Flow Estimation with Integrated Particle Reconstruction

The standard approach to densely reconstruct the motion in a volume of fluid is to inject high-contrast tracer particles and record their motion with multiple high-speed cameras. Almost all existing work processes the acquired multi-view video in two separate steps: first, a per-frame reconstruction of the particles, usually in the form of soft occupancy likelihoods in a voxel representation; followed by 3D motion estimation, with some form of dense matching between the precomputed voxel grids from different time steps. In this sequential procedure, the first step cannot use temporal consistency considerations to support the reconstruction, while the second step has no access to the original, high-resolution image data. We show, for the first time, how to jointly reconstruct both the individual tracer particles and a dense 3D fluid motion field from the image data, using an integrated energy minimization. Our hybrid Lagrangian/Eulerian model explicitly reconstructs individual particles, and at the same time recovers a dense 3D motion field in the entire domain. Making particles explicit greatly reduces the memory consumption and allows one to use the high-resolution input images for matching. Whereas the dense motion field makes it possible to include physical a-priori constraints and account for the incompressibility and viscosity of the fluid. The method exhibits greatly (~70%) improved results over a recent baseline with two separate steps for 3D reconstruction and motion estimation. Our results with only two time steps are comparable to those of state-of-the-art tracking-based methods that require much longer sequences.

Variational 3D-PIV with Sparse Descriptors

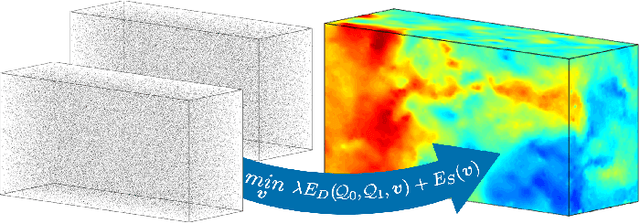
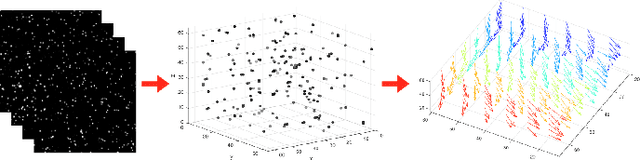
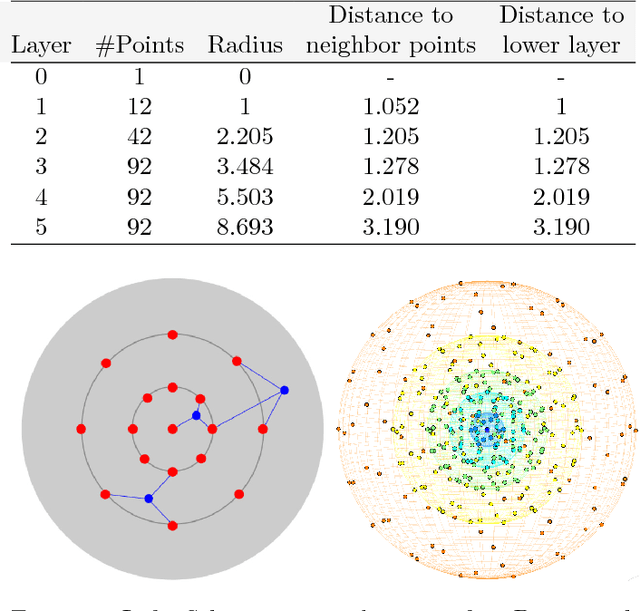
3D Particle Imaging Velocimetry (3D-PIV) aim to recover the flow field in a volume of fluid, which has been seeded with tracer particles and observed from multiple camera viewpoints. The first step of 3D-PIV is to reconstruct the 3D locations of the tracer particles from synchronous views of the volume. We propose a new method for iterative particle reconstruction (IPR), in which the locations and intensities of all particles are inferred in one joint energy minimization. The energy function is designed to penalize deviations between the reconstructed 3D particles and the image evidence, while at the same time aiming for a sparse set of particles. We find that the new method, without any post-processing, achieves significantly cleaner particle volumes than a conventional, tomographic MART reconstruction, and can handle a wide range of particle densities. The second step of 3D-PIV is to then recover the dense motion field from two consecutive particle reconstructions. We propose a variational model, which makes it possible to directly include physical properties, such as incompressibility and viscosity, in the estimation of the motion field. To further exploit the sparse nature of the input data, we propose a novel, compact descriptor of the local particle layout. Hence, we avoid the memory-intensive storage of high-resolution intensity volumes. Our framework is generic and allows for a variety of different data costs (correlation measures) and regularizers. We quantitatively evaluate it with both the sum of squared differences (SSD) and the normalized cross-correlation (NCC), respectively with both a hard and a soft version of the incompressibility constraint.