Katharina Küchler
Deep Koopman with Control: Spectral Analysis of Soft Robot Dynamics
Oct 14, 2022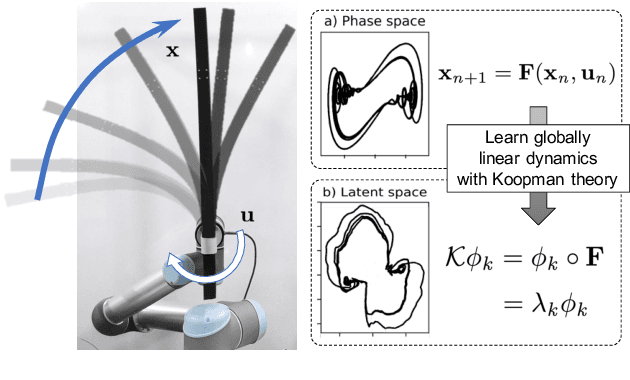
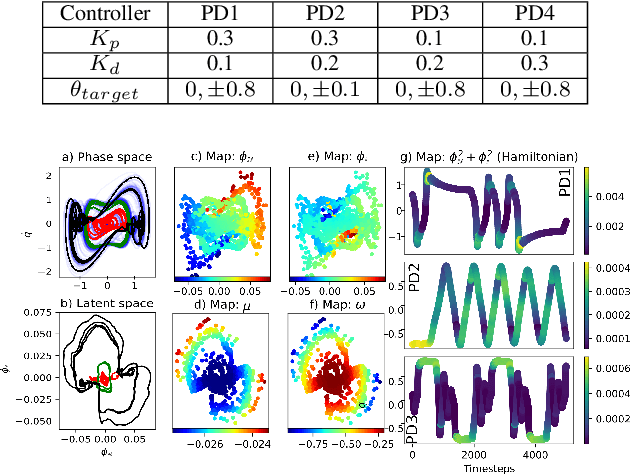
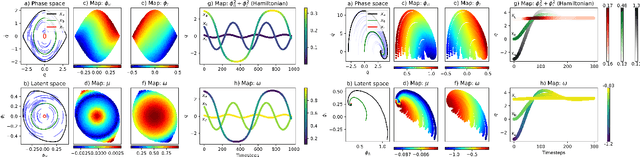

Abstract:Soft robots are challenging to model and control as inherent non-linearities (e.g., elasticity and deformation), often requires complex explicit physics-based analytical modeling (e.g., a priori geometric definitions). While machine learning can be used to learn non-linear control models in a data-driven approach, these models often lack an intuitive internal physical interpretation and representation, limiting dynamical analysis. To address this, this paper presents an approach using Koopman operator theory and deep neural networks to provide a global linear description of the non-linear control systems. Specifically, by globally linearising dynamics, the Koopman operator is analyzed using spectral decomposition to characterises important physics-based interpretations, such as functional growths and oscillations. Experiments in this paper demonstrate this approach for controlling non-linear soft robotics, and shows model outputs are interpretable in the context of spectral analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge