A Granular Framework for Construction Material Price Forecasting: Econometric and Machine-Learning Approaches

The persistent volatility of construction material prices poses significant risks to cost estimation, budgeting, and project delivery, underscoring the urgent need for granular and scalable forecasting methods. This study develops a forecasting framework that leverages the Construction Specifications Institute (CSI) MasterFormat as the target data structure, enabling predictions at the six-digit section level and supporting detailed cost projections across a wide spectrum of building materials. To enhance predictive accuracy, the framework integrates explanatory variables such as raw material prices, commodity indexes, and macroeconomic indicators. Four time-series models, Long Short-Term Memory (LSTM), Autoregressive Integrated Moving Average (ARIMA), Vector Error Correction Model (VECM), and Chronos-Bolt, were evaluated under both baseline configurations (using CSI data only) and extended versions with explanatory variables. Results demonstrate that incorporating explanatory variables significantly improves predictive performance across all models. Among the tested approaches, the LSTM model consistently achieved the highest accuracy, with RMSE values as low as 1.390 and MAPE values of 0.957, representing improvements of up to 59\% over the traditional statistical time-series model, ARIMA. Validation across multiple CSI divisions confirmed the framework's scalability, while Division 06 (Wood, Plastics, and Composites) is presented in detail as a demonstration case. This research offers a robust methodology that enables owners and contractors to improve budgeting practices and achieve more reliable cost estimation at the Definitive level.

Statistical learning method for predicting density-matrix based electron dynamics

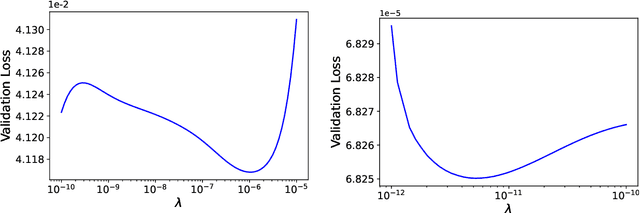
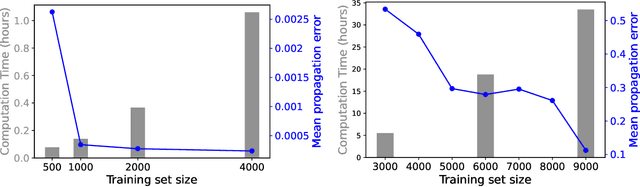
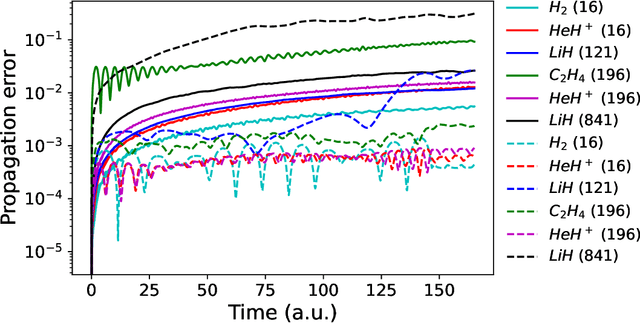
We develop a statistical method to learn a molecular Hamiltonian matrix from a time-series of electron density matrices. We extend our previous method to larger molecular systems by incorporating physical properties to reduce dimensionality, while also exploiting regularization techniques like ridge regression for addressing multicollinearity. With the learned Hamiltonian we can solve the Time-Dependent Hartree-Fock (TDHF) equation to propagate the electron density in time, and predict its dynamics for field-free and field-on scenarios. We observe close quantitative agreement between the predicted dynamics and ground truth for both field-off trajectories similar to the training data, and field-on trajectories outside of the training data.

Machine Learning a Molecular Hamiltonian for Predicting Electron Dynamics

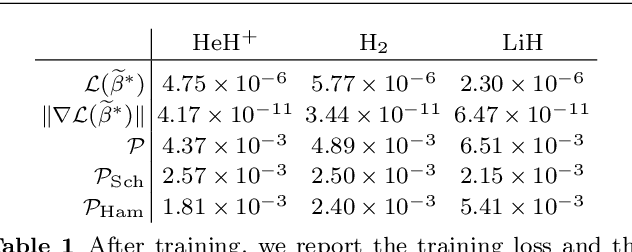
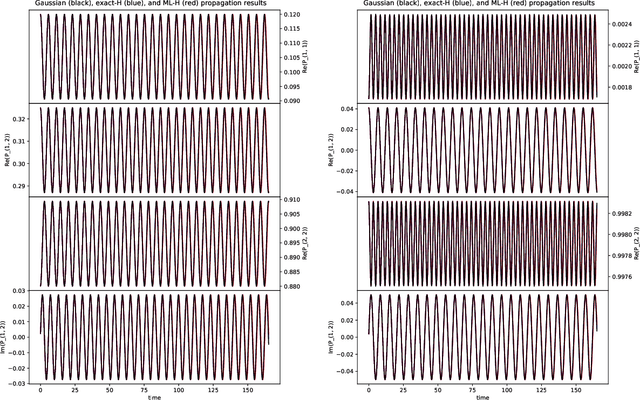
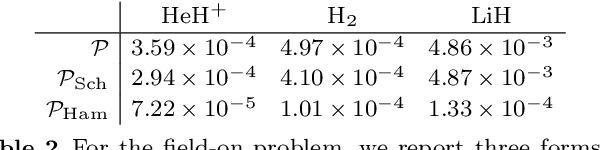
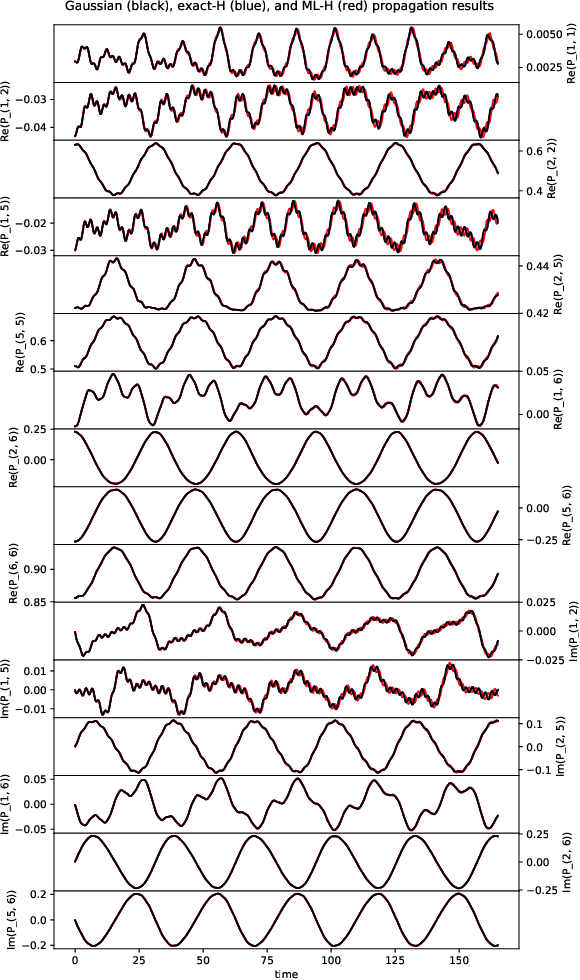
We develop a computational method to learn a molecular Hamiltonian matrix from matrix-valued time series of the electron density. As we demonstrate for three small molecules, the resulting Hamiltonians can be used for electron density evolution, producing highly accurate results even when propagating 1000 time steps beyond the training data. As a more rigorous test, we use the learned Hamiltonians to simulate electron dynamics in the presence of an applied electric field, extrapolating to a problem that is beyond the field-free training data. We find that the resulting electron dynamics predicted by our learned Hamiltonian are in close quantitative agreement with the ground truth. Our method relies on combining a reduced-dimensional, linear statistical model of the Hamiltonian with a time-discretization of the quantum Liouville equation within time-dependent Hartree Fock theory. We train the model using a least-squares solver, avoiding numerous, CPU-intensive optimization steps. For both field-free and field-on problems, we quantify training and propagation errors, highlighting areas for future development.