Scalable learning of potentials to predict time-dependent Hartree-Fock dynamics

We propose a framework to learn the time-dependent Hartree-Fock (TDHF) inter-electronic potential of a molecule from its electron density dynamics. Though the entire TDHF Hamiltonian, including the inter-electronic potential, can be computed from first principles, we use this problem as a testbed to develop strategies that can be applied to learn \emph{a priori} unknown terms that arise in other methods/approaches to quantum dynamics, e.g., emerging problems such as learning exchange-correlation potentials for time-dependent density functional theory. We develop, train, and test three models of the TDHF inter-electronic potential, each parameterized by a four-index tensor of size up to $60 \times 60 \times 60 \times 60$. Two of the models preserve Hermitian symmetry, while one model preserves an eight-fold permutation symmetry that implies Hermitian symmetry. Across seven different molecular systems, we find that accounting for the deeper eight-fold symmetry leads to the best-performing model across three metrics: training efficiency, test set predictive power, and direct comparison of true and learned inter-electronic potentials. All three models, when trained on ensembles of field-free trajectories, generate accurate electron dynamics predictions even in a field-on regime that lies outside the training set. To enable our models to scale to large molecular systems, we derive expressions for Jacobian-vector products that enable iterative, matrix-free training.

Dynamic Learning of Correlation Potentials for a Time-Dependent Kohn-Sham System

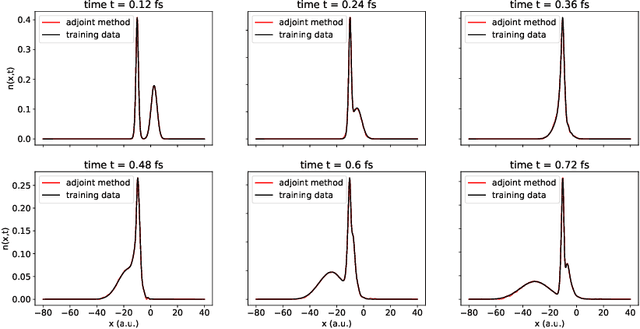
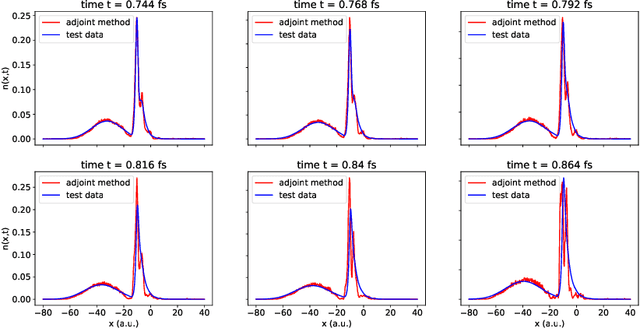
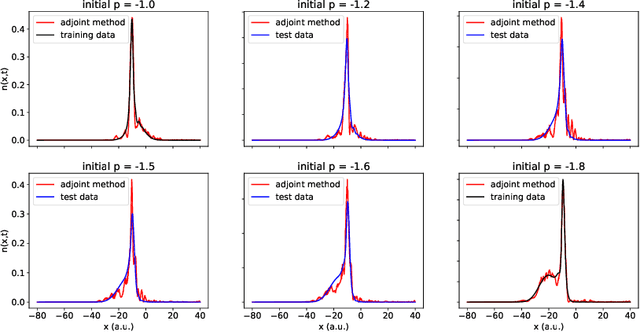
We develop methods to learn the correlation potential for a time-dependent Kohn-Sham (TDKS) system in one spatial dimension. We start from a low-dimensional two-electron system for which we can numerically solve the time-dependent Schr\"odinger equation; this yields electron densities suitable for training models of the correlation potential. We frame the learning problem as one of optimizing a least-squares objective subject to the constraint that the dynamics obey the TDKS equation. Applying adjoints, we develop efficient methods to compute gradients and thereby learn models of the correlation potential. Our results show that it is possible to learn values of the correlation potential such that the resulting electron densities match ground truth densities. We also show how to learn correlation potential functionals with memory, demonstrating one such model that yields reasonable results for trajectories outside the training set.

Training Dynamic based data filtering may not work for NLP datasets

The recent increase in dataset size has brought about significant advances in natural language understanding. These large datasets are usually collected through automation (search engines or web crawlers) or crowdsourcing which inherently introduces incorrectly labeled data. Training on these datasets leads to memorization and poor generalization. Thus, it is pertinent to develop techniques that help in the identification and isolation of mislabelled data. In this paper, we study the applicability of the Area Under the Margin (AUM) metric to identify and remove/rectify mislabelled examples in NLP datasets. We find that mislabelled samples can be filtered using the AUM metric in NLP datasets but it also removes a significant number of correctly labeled points and leads to the loss of a large amount of relevant language information. We show that models rely on the distributional information instead of relying on syntactic and semantic representations.

Statistical learning method for predicting density-matrix based electron dynamics

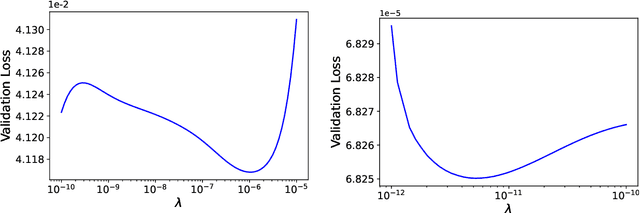
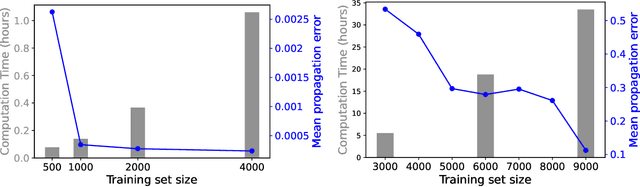
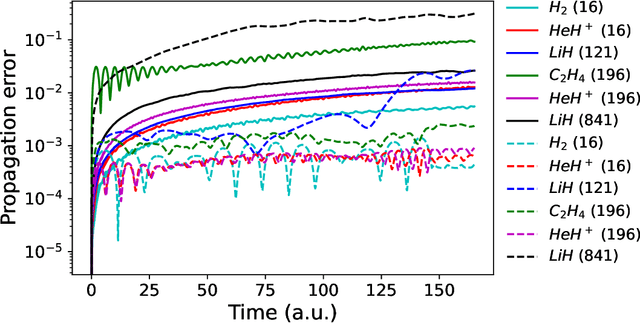
We develop a statistical method to learn a molecular Hamiltonian matrix from a time-series of electron density matrices. We extend our previous method to larger molecular systems by incorporating physical properties to reduce dimensionality, while also exploiting regularization techniques like ridge regression for addressing multicollinearity. With the learned Hamiltonian we can solve the Time-Dependent Hartree-Fock (TDHF) equation to propagate the electron density in time, and predict its dynamics for field-free and field-on scenarios. We observe close quantitative agreement between the predicted dynamics and ground truth for both field-off trajectories similar to the training data, and field-on trajectories outside of the training data.