Machine Learning a Molecular Hamiltonian for Predicting Electron Dynamics
Paper and Code
Aug 31, 2020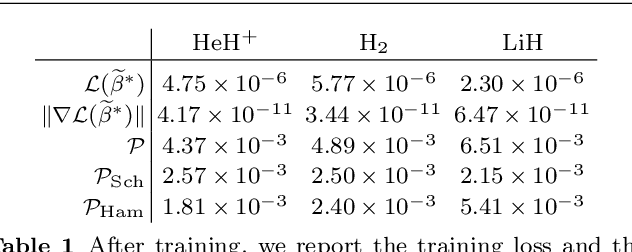
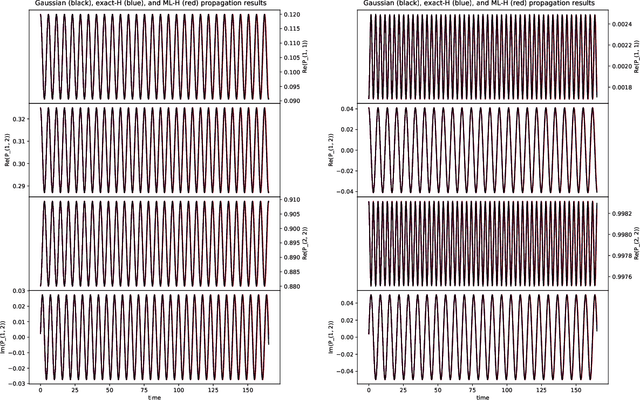
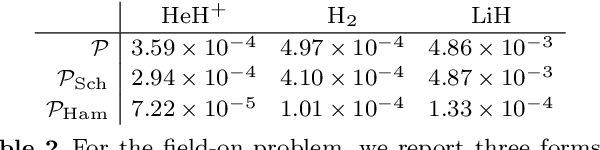
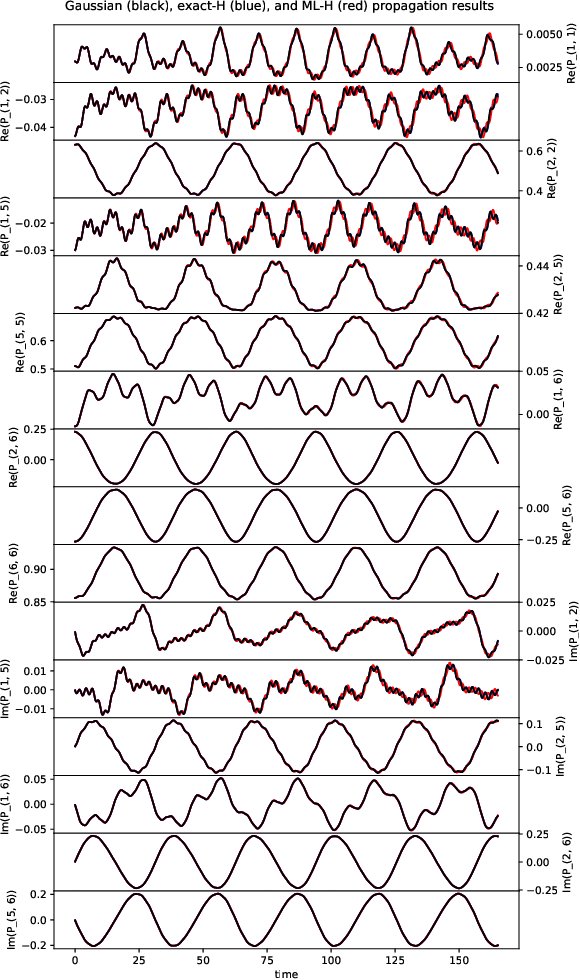
We develop a computational method to learn a molecular Hamiltonian matrix from matrix-valued time series of the electron density. As we demonstrate for three small molecules, the resulting Hamiltonians can be used for electron density evolution, producing highly accurate results even when propagating 1000 time steps beyond the training data. As a more rigorous test, we use the learned Hamiltonians to simulate electron dynamics in the presence of an applied electric field, extrapolating to a problem that is beyond the field-free training data. We find that the resulting electron dynamics predicted by our learned Hamiltonian are in close quantitative agreement with the ground truth. Our method relies on combining a reduced-dimensional, linear statistical model of the Hamiltonian with a time-discretization of the quantum Liouville equation within time-dependent Hartree Fock theory. We train the model using a least-squares solver, avoiding numerous, CPU-intensive optimization steps. For both field-free and field-on problems, we quantify training and propagation errors, highlighting areas for future development.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge