Kana Shimizu
Differentially private cross-silo federated learning
Jul 10, 2020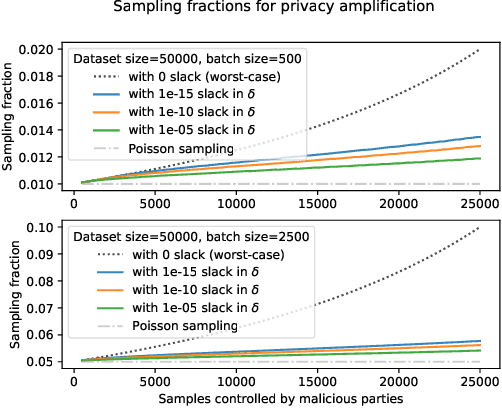
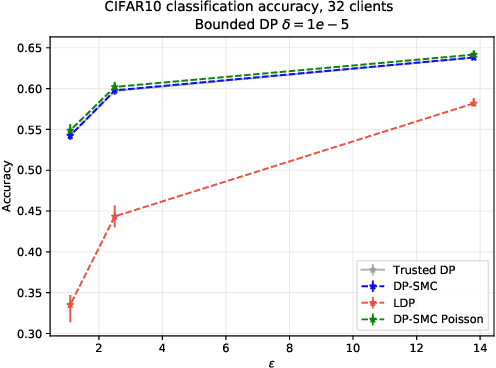
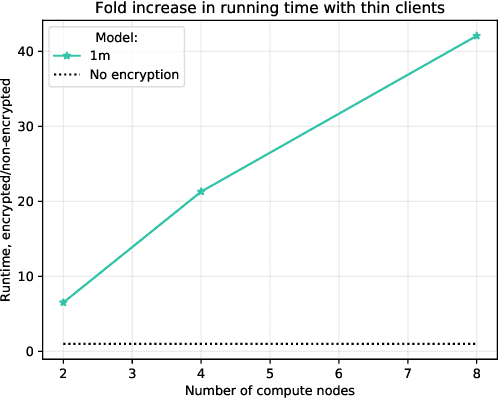
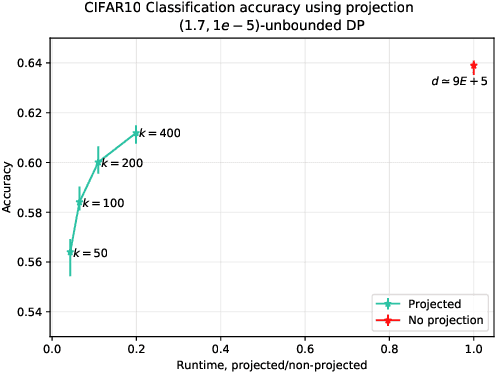
Abstract:Strict privacy is of paramount importance in distributed machine learning. Federated learning, with the main idea of communicating only what is needed for learning, has been recently introduced as a general approach for distributed learning to enhance learning and improve security. However, federated learning by itself does not guarantee any privacy for data subjects. To quantify and control how much privacy is compromised in the worst-case, we can use differential privacy. In this paper we combine additively homomorphic secure summation protocols with differential privacy in the so-called cross-silo federated learning setting. The goal is to learn complex models like neural networks while guaranteeing strict privacy for the individual data subjects. We demonstrate that our proposed solutions give prediction accuracy that is comparable to the non-distributed setting, and are fast enough to enable learning models with millions of parameters in a reasonable time. To enable learning under strict privacy guarantees that need privacy amplification by subsampling, we present a general algorithm for oblivious distributed subsampling. However, we also argue that when malicious parties are present, a simple approach using distributed Poisson subsampling gives better privacy. Finally, we show that by leveraging random projections we can further scale-up our approach to larger models while suffering only a modest performance loss.
Differentially Private Bayesian Learning on Distributed Data
May 29, 2017



Abstract:Many applications of machine learning, for example in health care, would benefit from methods that can guarantee privacy of data subjects. Differential privacy (DP) has become established as a standard for protecting learning results. The standard DP algorithms require a single trusted party to have access to the entire data, which is a clear weakness. We consider DP Bayesian learning in a distributed setting, where each party only holds a single sample or a few samples of the data. We propose a learning strategy based on a secure multi-party sum function for aggregating summaries from data holders and the Gaussian mechanism for DP. Our method builds on an asymptotically optimal and practically efficient DP Bayesian inference with rapidly diminishing extra cost.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge