LIBS2ML: A Library for Scalable Second Order Machine Learning Algorithms

LIBS2ML is a library based on scalable second order learning algorithms for solving large-scale problems, i.e., big data problems in machine learning. LIBS2ML has been developed using MEX files, i.e., C++ with MATLAB/Octave interface to take the advantage of both the worlds, i.e., faster learning using C++ and easy I/O using MATLAB. Most of the available libraries are either in MATLAB/Python/R which are very slow and not suitable for large-scale learning, or are in C/C++ which does not have easy ways to take input and display results. So LIBS2ML is completely unique due to its focus on the scalable second order methods, the hot research topic, and being based on MEX files. Thus it provides researchers a comprehensive environment to evaluate their ideas and it also provides machine learning practitioners an effective tool to deal with the large-scale learning problems. LIBS2ML is an open-source, highly efficient, extensible, scalable, readable, portable and easy to use library. The library can be downloaded from the URL: \url{https://github.com/jmdvinodjmd/LIBS2ML}.

Stochastic Trust Region Inexact Newton Method for Large-scale Machine Learning

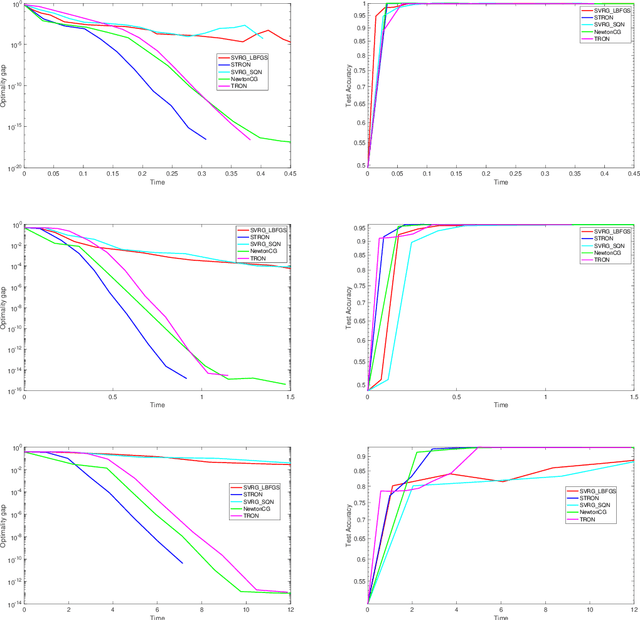
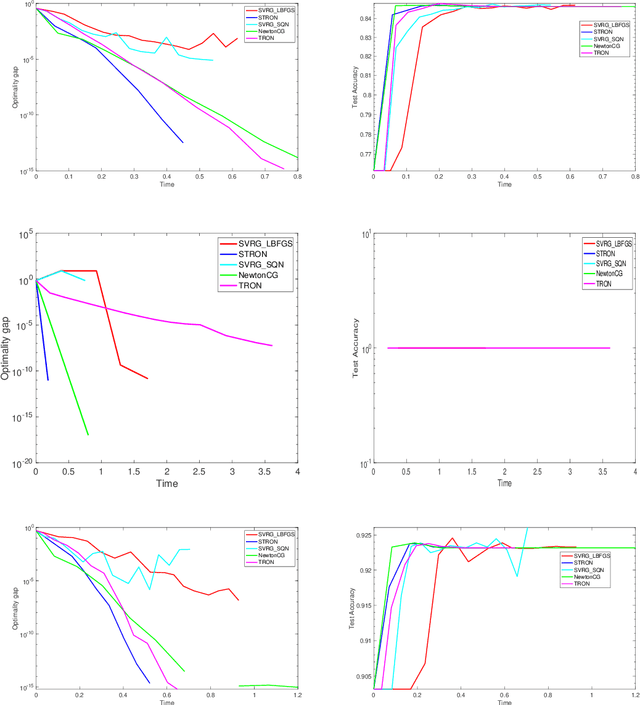
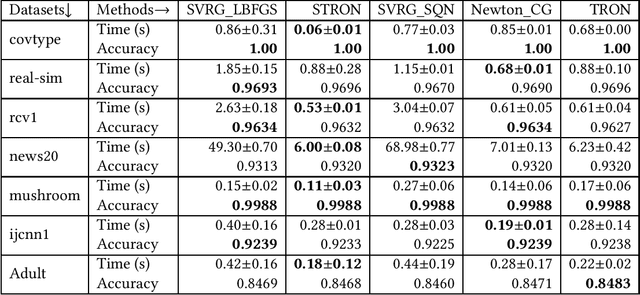
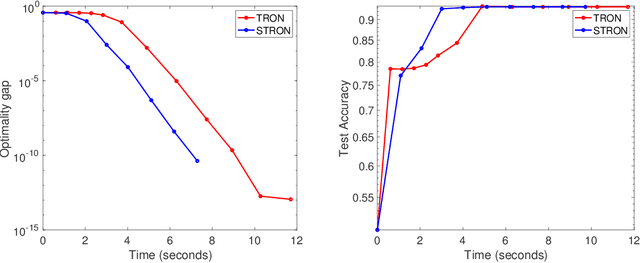
Nowadays stochastic approximation methods are one of the major research direction to deal with the large-scale machine learning problems. From stochastic first order methods, now the focus is shifting to stochastic second order methods due to their faster convergence. In this paper, we have proposed a novel Stochastic Trust RegiOn inexact Newton method, called as STRON, which uses conjugate gradient (CG) to solve trust region subproblem. The method uses progressive subsampling in the calculation of gradient and Hessian values to take the advantage of both stochastic approximation and full batch regimes. We have extended STRON using existing variance reduction techniques to deal with the noisy gradients, and using preconditioned conjugate gradient (PCG) as subproblem solver. We further extend STRON to solve SVM. Finally, the theoretical results prove superlinear convergence for STRON and the empirical results prove the efficacy of the proposed method against existing methods with bench marked datasets.

Faster Learning by Reduction of Data Access Time

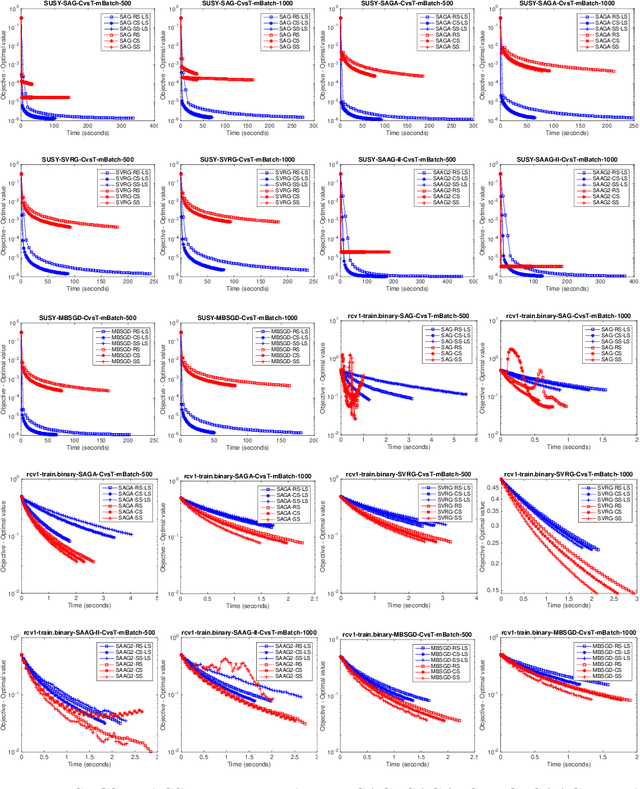
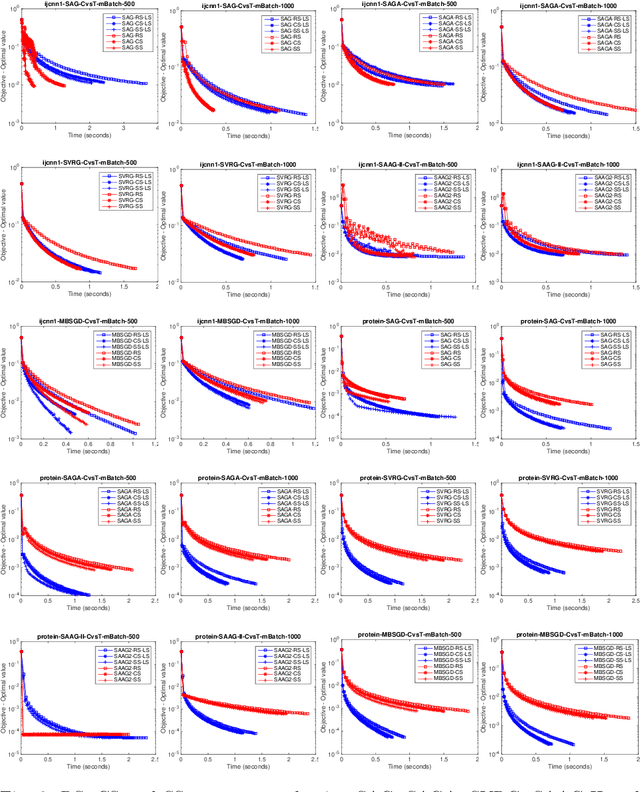
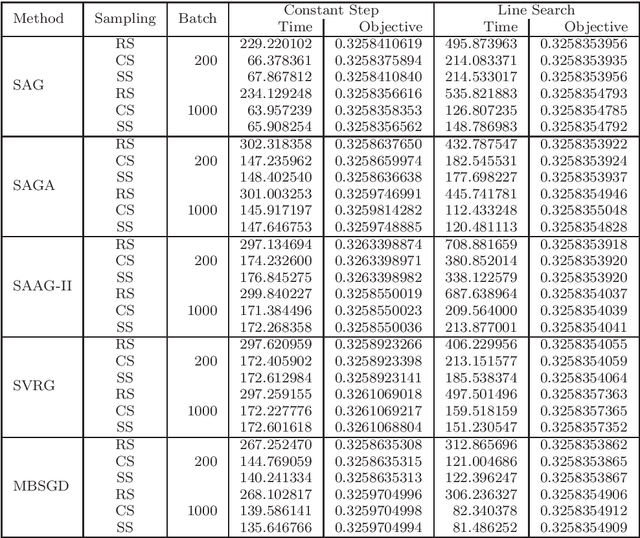
Nowadays, the major challenge in machine learning is the Big Data challenge. The big data problems due to large number of data points or large number of features in each data point, or both, the training of models have become very slow. The training time has two major components: Time to access the data and time to process (learn from) the data. So far, the research has focused only on the second part, i.e., learning from the data. In this paper, we have proposed one possible solution to handle the big data problems in machine learning. The idea is to reduce the training time through reducing data access time by proposing systematic sampling and cyclic/sequential sampling to select mini-batches from the dataset. To prove the effectiveness of proposed sampling techniques, we have used Empirical Risk Minimization, which is commonly used machine learning problem, for strongly convex and smooth case. The problem has been solved using SAG, SAGA, SVRG, SAAG-II and MBSGD (Mini-batched SGD), each using two step determination techniques, namely, constant step size and backtracking line search method. Theoretical results prove the same convergence for systematic sampling, cyclic sampling and the widely used random sampling technique, in expectation. Experimental results with bench marked datasets prove the efficacy of the proposed sampling techniques and show up to six times faster training.

SAAGs: Biased Stochastic Variance Reduction Methods

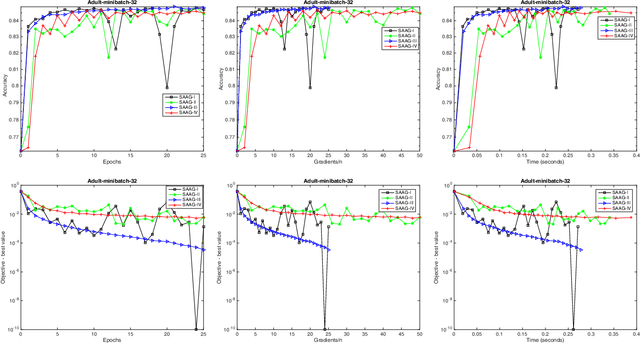
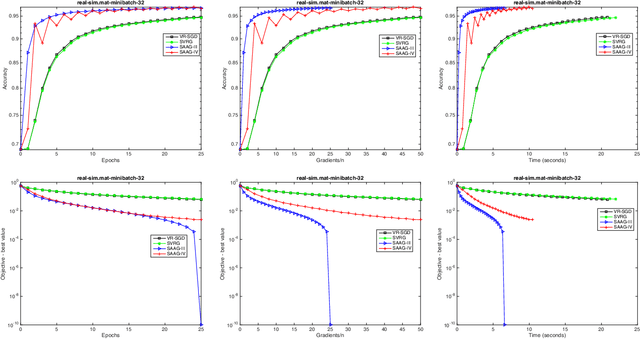
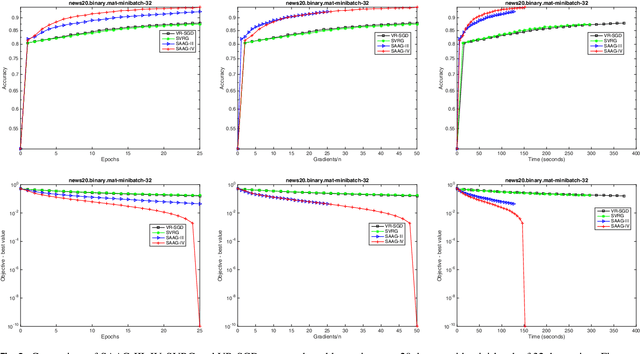
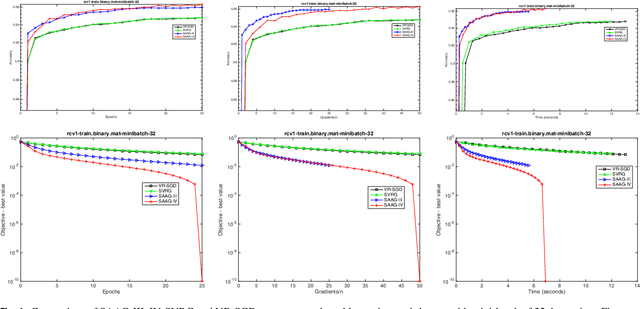
Stochastic optimization is one of the effective approach to deal with the large-scale machine learning problems and the recent research has focused on reduction of variance, caused by the noisy approximations of the gradients, and momentum acceleration. In this paper, we have proposed simple variants of SAAG-I and II (Stochastic Average Adjusted Gradient) \cite{Chauhan2017Saag}, called SAAG-III and IV, respectively. Unlike SAAG-I, starting point is set to average of previous epoch in SAAG-III, and unlike SAAG-II, the snap point and starting point are set to average and last iterate of previous epoch, respectively. To determine the step size, we introduce Stochastic Backtracking-Armijo line Search (SBAS) which performs line search only on selected mini-batch of data points. Since backtracking line search is not suitable for large-scale problems and the constants used to find the step size, like Lipschitz constant, are not always available so SBAS could be very effective in such cases. We also extend SAAGs (I, II, III, IV), to solve non-smooth problems and design two update rules for smooth and non-smooth problems. Moreover, our theoretical results prove linear convergence of SAAG-IV for all the four combinations of smoothness and strong-convexity, in expectation. Finally, our experimental studies prove the efficacy of proposed methods against the state-of-art techniques, like, SVRG and VR-SGD.