SAAGs: Biased Stochastic Variance Reduction Methods

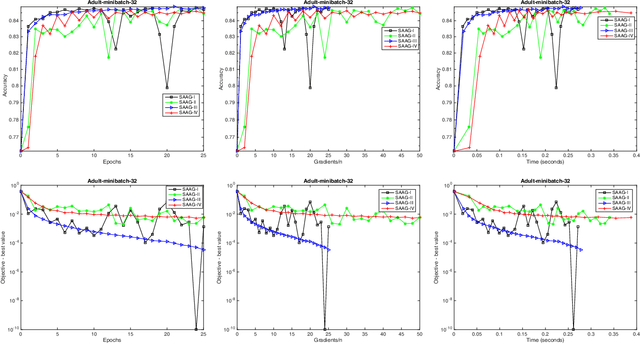
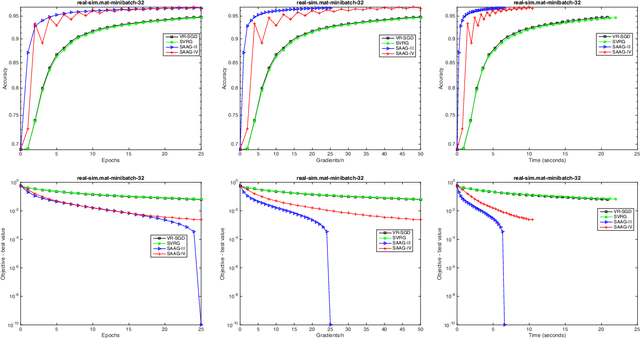
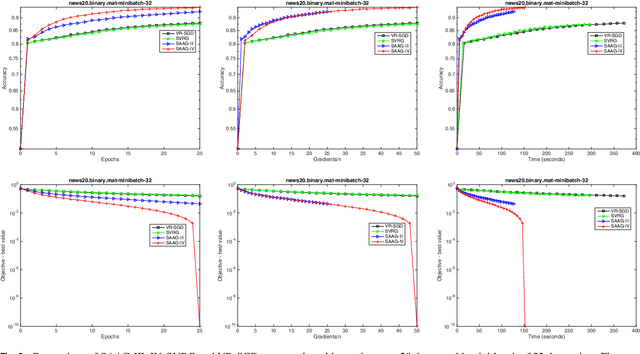
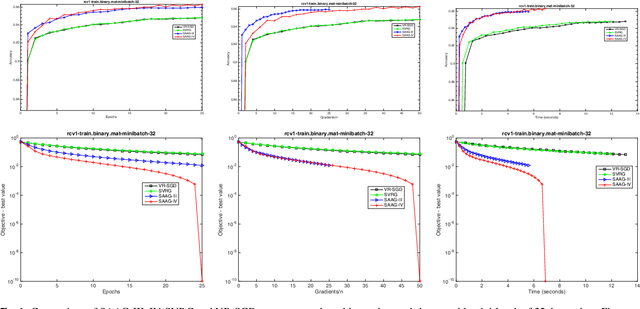
Stochastic optimization is one of the effective approach to deal with the large-scale machine learning problems and the recent research has focused on reduction of variance, caused by the noisy approximations of the gradients, and momentum acceleration. In this paper, we have proposed simple variants of SAAG-I and II (Stochastic Average Adjusted Gradient) \cite{Chauhan2017Saag}, called SAAG-III and IV, respectively. Unlike SAAG-I, starting point is set to average of previous epoch in SAAG-III, and unlike SAAG-II, the snap point and starting point are set to average and last iterate of previous epoch, respectively. To determine the step size, we introduce Stochastic Backtracking-Armijo line Search (SBAS) which performs line search only on selected mini-batch of data points. Since backtracking line search is not suitable for large-scale problems and the constants used to find the step size, like Lipschitz constant, are not always available so SBAS could be very effective in such cases. We also extend SAAGs (I, II, III, IV), to solve non-smooth problems and design two update rules for smooth and non-smooth problems. Moreover, our theoretical results prove linear convergence of SAAG-IV for all the four combinations of smoothness and strong-convexity, in expectation. Finally, our experimental studies prove the efficacy of proposed methods against the state-of-art techniques, like, SVRG and VR-SGD.