Faster Learning by Reduction of Data Access Time

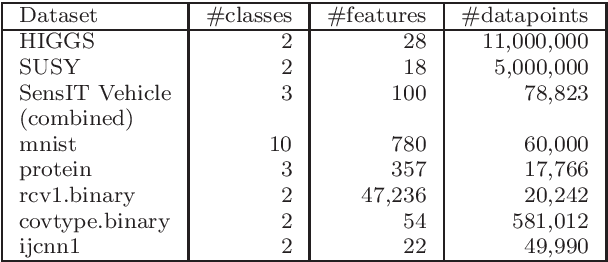
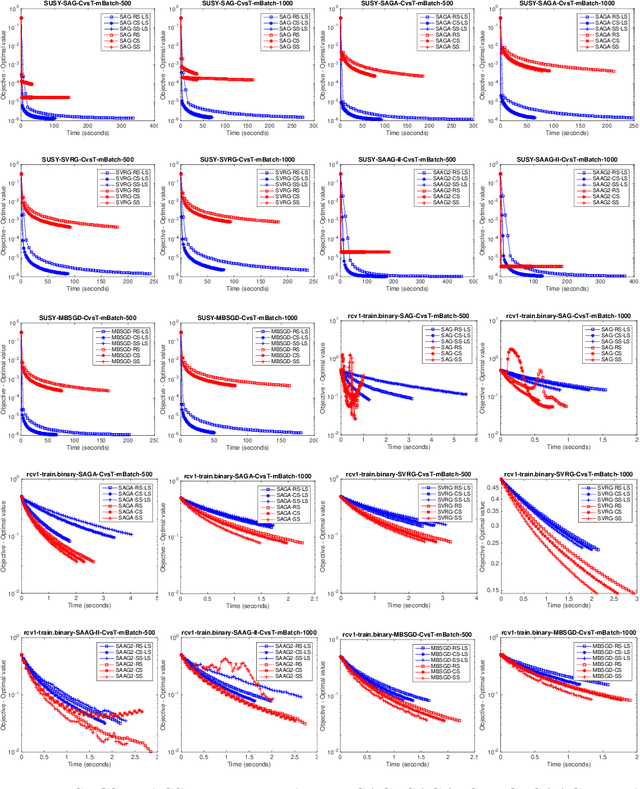
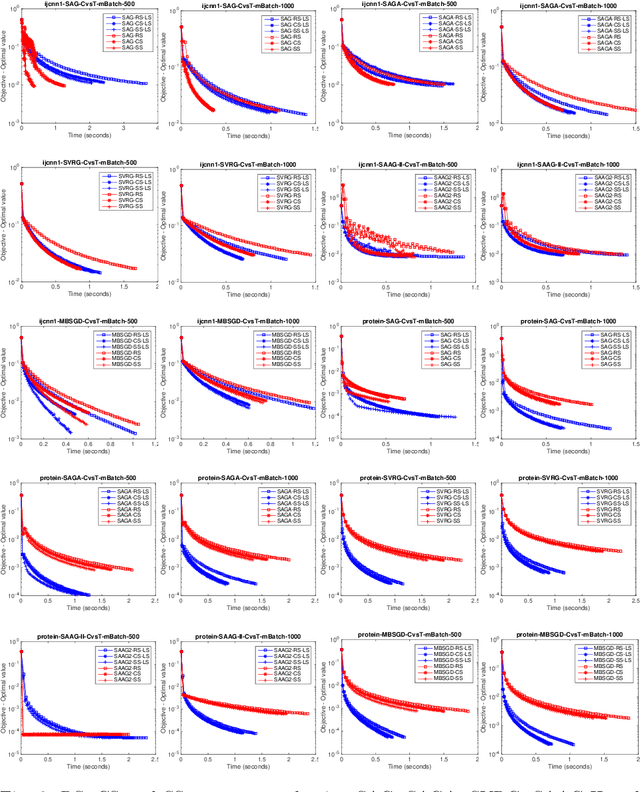
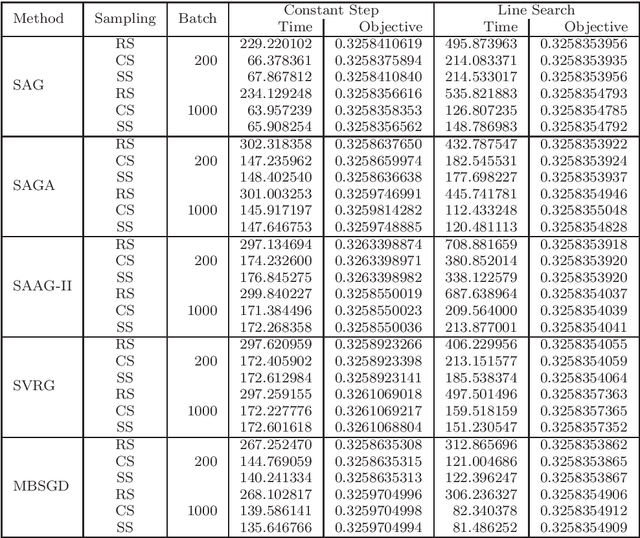
Nowadays, the major challenge in machine learning is the Big Data challenge. The big data problems due to large number of data points or large number of features in each data point, or both, the training of models have become very slow. The training time has two major components: Time to access the data and time to process (learn from) the data. So far, the research has focused only on the second part, i.e., learning from the data. In this paper, we have proposed one possible solution to handle the big data problems in machine learning. The idea is to reduce the training time through reducing data access time by proposing systematic sampling and cyclic/sequential sampling to select mini-batches from the dataset. To prove the effectiveness of proposed sampling techniques, we have used Empirical Risk Minimization, which is commonly used machine learning problem, for strongly convex and smooth case. The problem has been solved using SAG, SAGA, SVRG, SAAG-II and MBSGD (Mini-batched SGD), each using two step determination techniques, namely, constant step size and backtracking line search method. Theoretical results prove the same convergence for systematic sampling, cyclic sampling and the widely used random sampling technique, in expectation. Experimental results with bench marked datasets prove the efficacy of the proposed sampling techniques and show up to six times faster training.