A Novel Fuzzy Bi-Clustering Algorithm with AFS for Identification of Co-Regulated Genes

The identification of co-regulated genes and their transcription-factor binding sites (TFBS) are the key steps toward understanding transcription regulation. In addition to effective laboratory assays, various bi-clustering algorithms for detection of the co-expressed genes have been developed. Bi-clustering methods are used to discover subgroups of genes with similar expression patterns under to-be-identified subsets of experimental conditions when applied to gene expression data. By building two fuzzy partition matrices of the gene expression data with the Axiomatic Fuzzy Set (AFS) theory, this paper proposes a novel fuzzy bi-clustering algorithm for identification of co-regulated genes. Specifically, the gene expression data is transformed into two fuzzy partition matrices via sub-preference relations theory of AFS at first. One of the matrices is considering the genes as the universe and the conditions as the concept, the other one is considering the genes as the concept and the conditions as the universe. The identification of the co-regulated genes (bi-clusters) is carried out on the two partition matrices at the same time. Then, a novel fuzzy-based similarity criterion is defined based on the partition matrixes, and a cyclic optimization algorithm is designed to discover the significant bi-clusters at expression level. The above procedures guarantee that the generated bi-clusters have more significant expression values than that of extracted by the traditional bi-clustering methods. Finally, the performance of the proposed method is evaluated with the performance of the three well-known bi-clustering algorithms on publicly available real microarray datasets. The experimental results are in agreement with the theoretical analysis and show that the proposed algorithm can effectively detect the co-regulated genes without any prior knowledge of the gene expression data.

An Enhanced Adaptive Bi-clustering Algorithm through Building a Shielding Complex Sub-Matrix

Bi-clustering refers to the task of finding sub-matrices (indexed by a group of columns and a group of rows) within a matrix of data such that the elements of each sub-matrix (data and features) are related in a particular way, for instance, that they are similar with respect to some metric. In this paper, after analyzing the well-known Cheng and Church (CC) bi-clustering algorithm which has been proved to be an effective tool for mining co-expressed genes. However, Cheng and Church bi-clustering algorithm and summarizing its limitations (such as interference of random numbers in the greedy strategy; ignoring overlapping bi-clusters), we propose a novel enhancement of the adaptive bi-clustering algorithm, where a shielding complex sub-matrix is constructed to shield the bi-clusters that have been obtained and to discover the overlapping bi-clusters. In the shielding complex sub-matrix, the imaginary and the real parts are used to shield and extend the new bi-clusters, respectively, and to form a series of optimal bi-clusters. To assure that the obtained bi-clusters have no effect on the bi-clusters already produced, a unit impulse signal is introduced to adaptively detect and shield the constructed bi-clusters. Meanwhile, to effectively shield the null data (zero-size data), another unit impulse signal is set for adaptive detecting and shielding. In addition, we add a shielding factor to adjust the mean squared residue score of the rows (or columns), which contains the shielded data of the sub-matrix, to decide whether to retain them or not. We offer a thorough analysis of the developed scheme. The experimental results are in agreement with the theoretical analysis. The results obtained on a publicly available real microarray dataset show the enhancement of the bi-clusters performance thanks to the proposed method.

Exploiting a Supervised Index for High-accuracy Parameter Estimation in Low SNR

Performance of parameter estimation is one of the most important issues in array signal processing. The root mean square error, probability of success, resolution probabilities, and computational complexity are frequently used indexes for evaluating the performance of the parameter estimation methods. However, a common characteristic of these indexes is that they are unsupervised indexes, and are passively used for evaluating the estimation results. In other words, these indexes cannot participate in the design of estimation methods. It seems that exploiting a validity supervised index for the parameter estimation that can guide the design of the methods will be an interesting and meaningful work. In this study, we exploit an index to build a supervised learning model of the parameter estimation. With the developed model we refine the signal subspace so as to enhance the performance of the parameter estimation method. The main characteristic of the proposed model is a circularly applied feedback of the estimated parameter for refining the estimated subspace. It is a closed loop and supervised method not reported before. This research opens a specific way for improving the performance of the parameter estimation by a supervised index. However, the proposed method is still unsatisfying in some scopes of signal-to-noise ratio (SNR). We believe that exploiting a validity index for the parameter estimation in array signal processing is still a general and interesting problem.

How to Determine an Optimal Noise Subspace?

The Multiple Signal Classification (MUSIC) algorithm based on the orthogonality between the signal subspace and noise subspace is one of the most frequently used method in the estimation of Direction Of Arrival (DOA), and its performance of DOA estimation mainly depends on the accuracy of the noise subspace. In the most existing researches, the noise subspace is formed by (defined as) the eigenvectors corresponding to all small eigenvalues of the array output covariance matrix. However, we found that the estimation of DOA through the noise subspace in the traditional formation is not optimal in almost all cases, and using a partial noise subspace can always obtain optimal estimation results. In other words, the subspace spanned by the eigenvectors corresponding to a part of the small eigenvalues is more representative of the noise subspace. We demonstrate this conclusion through a number of experiments. Thus, it seems that which and how many eigenvectors should be selected to form the partial noise subspace would be an interesting issue. In addition, this research poses a much general problem: how to select eigenvectors to determine an optimal noise subspace?

A Novel Granular-Based Bi-Clustering Method of Deep Mining the Co-Expressed Genes

Traditional clustering methods are limited when dealing with huge and heterogeneous groups of gene expression data, which motivates the development of bi-clustering methods. Bi-clustering methods are used to mine bi-clusters whose subsets of samples (genes) are co-regulated under their test conditions. Studies show that mining bi-clusters of consistent trends and trends with similar degrees of fluctuations from the gene expression data is essential in bioinformatics research. Unfortunately, traditional bi-clustering methods are not fully effective in discovering such bi-clusters. Therefore, we propose a novel bi-clustering method by involving here the theory of Granular Computing. In the proposed scheme, the gene data matrix, considered as a group of time series, is transformed into a series of ordered information granules. With the information granules we build a characteristic matrix of the gene data to capture the fluctuation trend of the expression value between consecutive conditions to mine the ideal bi-clusters. The experimental results are in agreement with the theoretical analysis, and show the excellent performance of the proposed method.

Augmentation of the Reconstruction Performance of Fuzzy C-Means with an Optimized Fuzzification Factor Vector

Information granules have been considered to be the fundamental constructs of Granular Computing (GrC). As a useful unsupervised learning technique, Fuzzy C-Means (FCM) is one of the most frequently used methods to construct information granules. The FCM-based granulation-degranulation mechanism plays a pivotal role in GrC. In this paper, to enhance the quality of the degranulation (reconstruction) process, we augment the FCM-based degranulation mechanism by introducing a vector of fuzzification factors (fuzzification factor vector) and setting up an adjustment mechanism to modify the prototypes and the partition matrix. The design is regarded as an optimization problem, which is guided by a reconstruction criterion. In the proposed scheme, the initial partition matrix and prototypes are generated by the FCM. Then a fuzzification factor vector is introduced to form an appropriate fuzzification factor for each cluster to build up an adjustment scheme of modifying the prototypes and the partition matrix. With the supervised learning mode of the granulation-degranulation process, we construct a composite objective function of the fuzzification factor vector, the prototypes and the partition matrix. Subsequently, the particle swarm optimization (PSO) is employed to optimize the fuzzification factor vector to refine the prototypes and develop the optimal partition matrix. Finally, the reconstruction performance of the FCM algorithm is enhanced. We offer a thorough analysis of the developed scheme. In particular, we show that the classical FCM algorithm forms a special case of the proposed scheme. Experiments completed for both synthetic and publicly available datasets show that the proposed approach outperforms the generic data reconstruction approach.

Granular Computing: An Augmented Scheme of Degranulation Through a Modified Partition Matrix

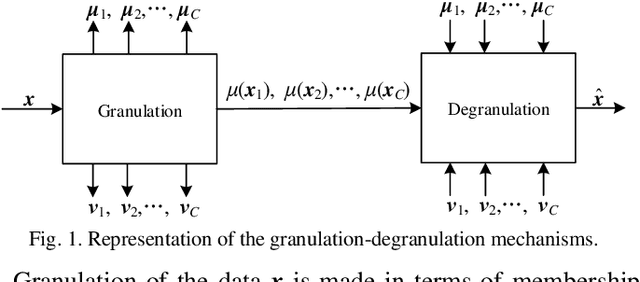
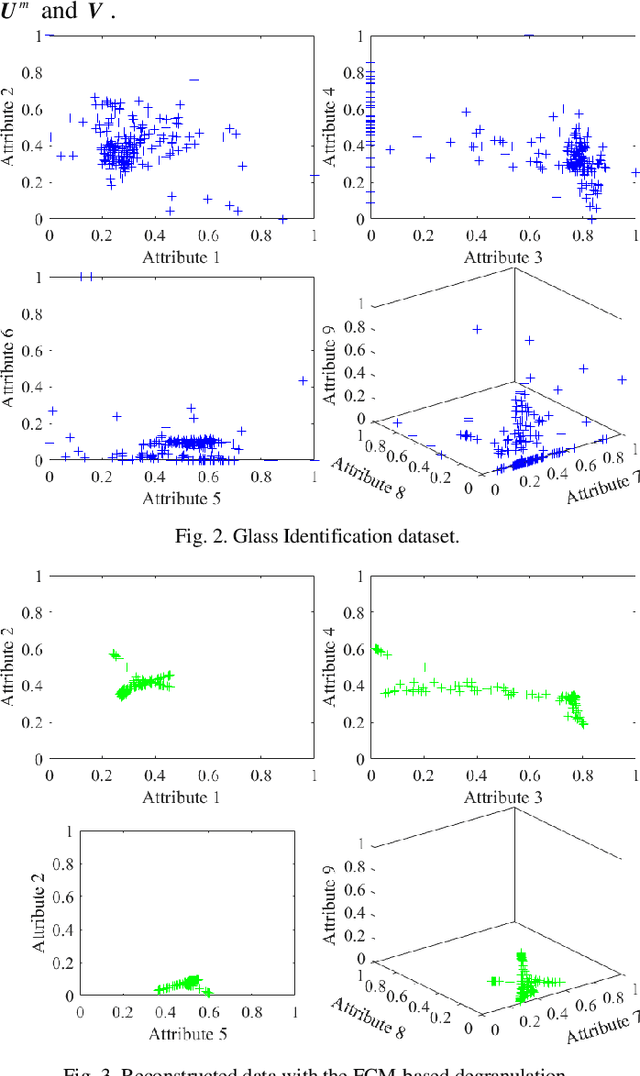
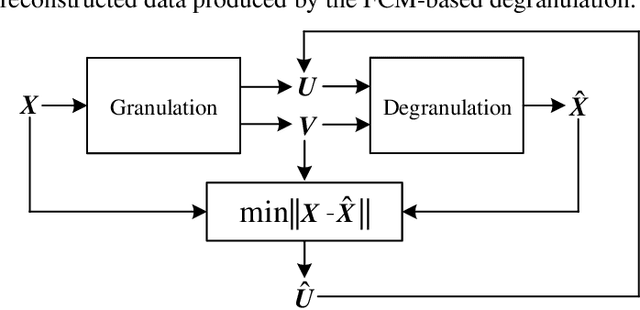
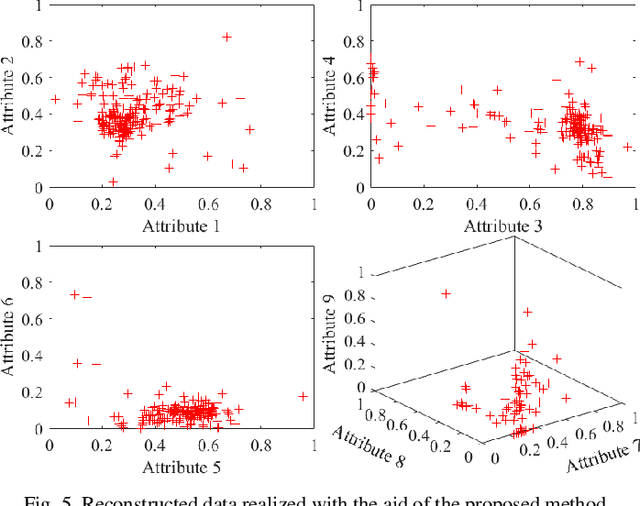
As an important technology in artificial intelligence Granular Computing (GrC) has emerged as a new multi-disciplinary paradigm and received much attention in recent years. Information granules forming an abstract and efficient characterization of large volumes of numeric data have been considered as the fundamental constructs of GrC. By generating prototypes and partition matrix, fuzzy clustering is a commonly encountered way of information granulation. Degranulation involves data reconstruction completed on a basis of the granular representatives. Previous studies have shown that there is a relationship between the reconstruction error and the performance of the granulation process. Typically, the lower the degranulation error is, the better performance of granulation is. However, the existing methods of degranulation usually cannot restore the original numeric data, which is one of the important reasons behind the occurrence of the reconstruction error. To enhance the quality of degranulation, in this study, we develop an augmented scheme through modifying the partition matrix. By proposing the augmented scheme, we dwell on a novel collection of granulation-degranulation mechanisms. In the constructed approach, the prototypes can be expressed as the product of the dataset matrix and the partition matrix. Then, in the degranulation process, the reconstructed numeric data can be decomposed into the product of the partition matrix and the matrix of prototypes. Both the granulation and degranulation are regarded as generalized rotation between the data subspace and the prototype subspace with the partition matrix and the fuzzification factor. By modifying the partition matrix, the new partition matrix is constructed through a series of matrix operations. We offer a thorough analysis of the developed scheme. The experimental results are in agreement with the underlying conceptual framework