Kai Haase
Neural Model-based Optimization with Right-Censored Observations
Sep 29, 2020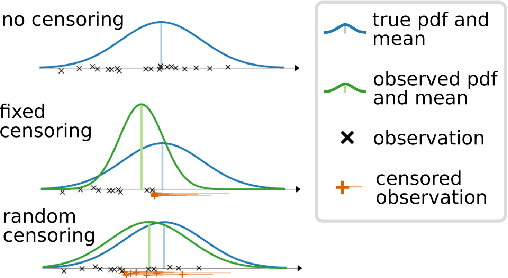
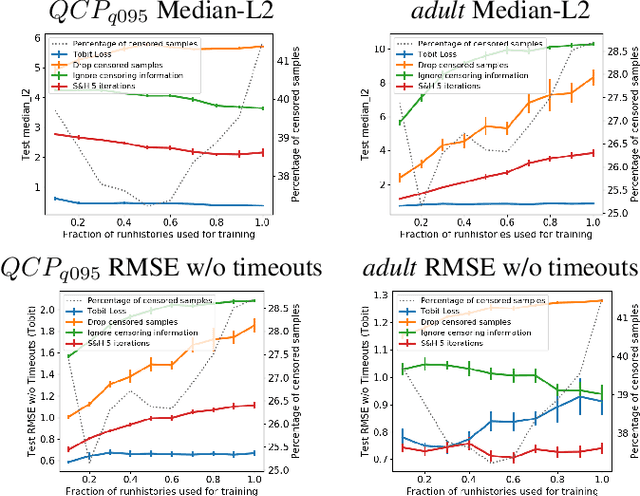

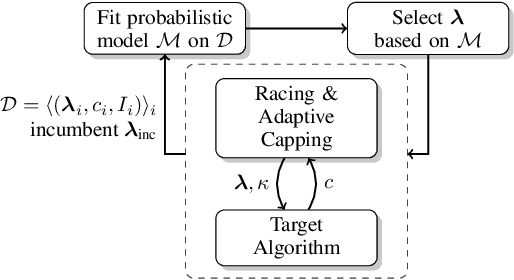
Abstract:In many fields of study, we only observe lower bounds on the true response value of some experiments. When fitting a regression model to predict the distribution of the outcomes, we cannot simply drop these right-censored observations, but need to properly model them. In this work, we focus on the concept of censored data in the light of model-based optimization where prematurely terminating evaluations (and thus generating right-censored data) is a key factor for efficiency, e.g., when searching for an algorithm configuration that minimizes runtime of the algorithm at hand. Neural networks (NNs) have been demonstrated to work well at the core of model-based optimization procedures and here we extend them to handle these censored observations. We propose (i)~a loss function based on the Tobit model to incorporate censored samples into training and (ii) use an ensemble of networks to model the posterior distribution. To nevertheless be efficient in terms of optimization-overhead, we propose to use Thompson sampling s.t. we only need to train a single NN in each iteration. Our experiments show that our trained regression models achieve a better predictive quality than several baselines and that our approach achieves new state-of-the-art performance for model-based optimization on two optimization problems: minimizing the solution time of a SAT solver and the time-to-accuracy of neural networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge