Unsupervised Training for Neural TSP Solver

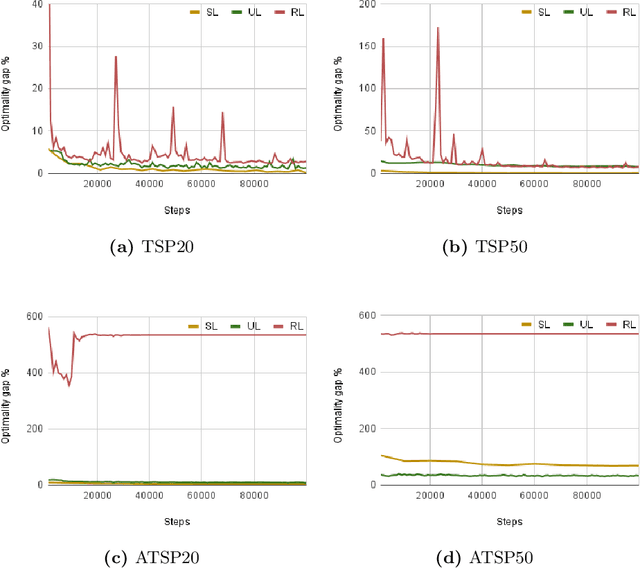
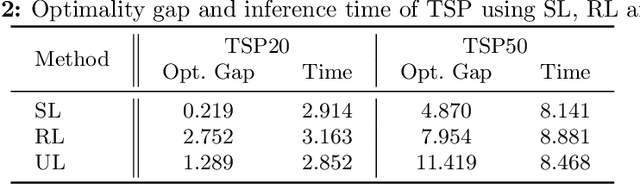
There has been a growing number of machine learning methods for approximately solving the travelling salesman problem. However, these methods often require solved instances for training or use complex reinforcement learning approaches that need a large amount of tuning. To avoid these problems, we introduce a novel unsupervised learning approach. We use a relaxation of an integer linear program for TSP to construct a loss function that does not require correct instance labels. With variable discretization, its minimum coincides with the optimal or near-optimal solution. Furthermore, this loss function is differentiable and thus can be used to train neural networks directly. We use our loss function with a Graph Neural Network and design controlled experiments on both Euclidean and asymmetric TSP. Our approach has the advantage over supervised learning of not requiring large labelled datasets. In addition, the performance of our approach surpasses reinforcement learning for asymmetric TSP and is comparable to reinforcement learning for Euclidean instances. Our approach is also more stable and easier to train than reinforcement learning.

Switchblade -- a Neural Network for Hard 2D Tasks

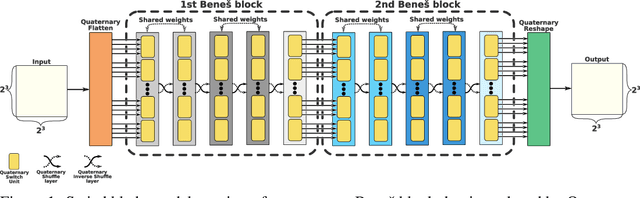
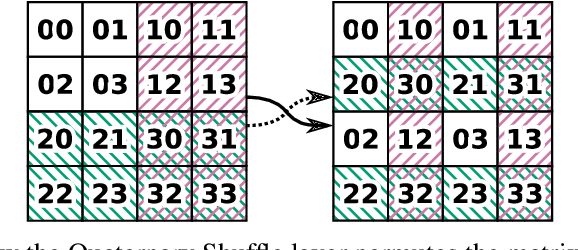
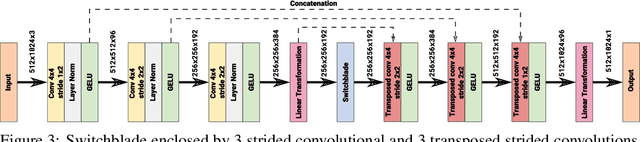
Convolutional neural networks have become the main tools for processing two-dimensional data. They work well for images, yet convolutions have a limited receptive field that prevents its applications to more complex 2D tasks. We propose a new neural network model, named Switchblade, that can efficiently exploit long-range dependencies in 2D data and solve much more challenging tasks. It has close-to-optimal $\mathcal{O}(n^2 \log{n})$ complexity for processing $n \times n$ data matrix. Besides the common image classification and segmentation, we consider a diverse set of algorithmic tasks on matrices and graphs. Switchblade can infer highly complex matrix squaring and graph triangle finding algorithms purely from input-output examples. We show that our model is likewise suitable for logical reasoning tasks -- it attains perfect accuracy on Sudoku puzzle solving. Additionally, we introduce a new dataset for predicting the checkmating move in chess on which our model achieves 72.5% accuracy.

Neural Shuffle-Exchange Networks -- Sequence Processing in O(n log n) Time

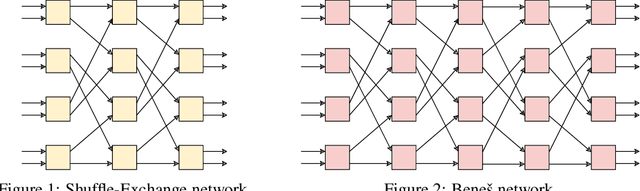
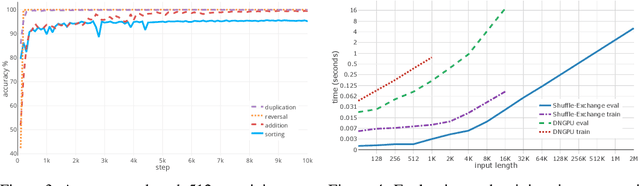
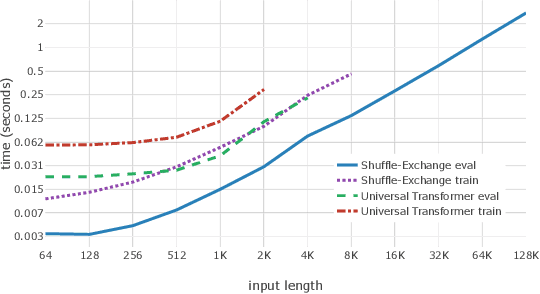
A key requirement in sequence to sequence processing is the modeling of long range dependencies. To this end, a vast majority of the state-of-the-art models use attention mechanism which is of O($n^2$) complexity that leads to slow execution for long sequences. We introduce a new Shuffle-Exchange neural network model for sequence to sequence tasks which have O(log n) depth and O(n log n) total complexity. We show that this model is powerful enough to infer efficient algorithms for common algorithmic benchmarks including sorting, addition and multiplication. We evaluate our architecture on the challenging LAMBADA question answering dataset and compare it with the state-of-the-art models which use attention. Our model achieves competitive accuracy and scales to sequences with more than a hundred thousand of elements. We are confident that the proposed model has the potential for building more efficient architectures for processing large interrelated data in language modeling, music generation and other application domains.