Switchblade -- a Neural Network for Hard 2D Tasks
Paper and Code
Jun 29, 2020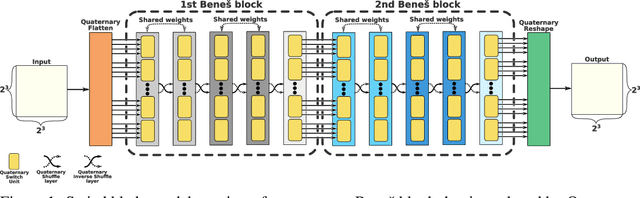

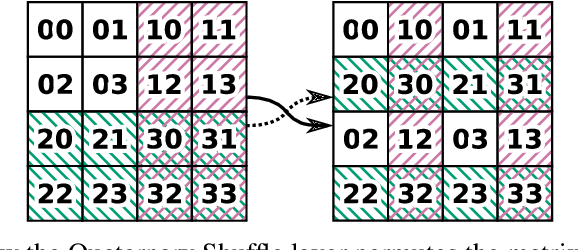
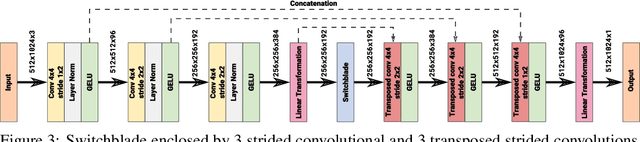
Convolutional neural networks have become the main tools for processing two-dimensional data. They work well for images, yet convolutions have a limited receptive field that prevents its applications to more complex 2D tasks. We propose a new neural network model, named Switchblade, that can efficiently exploit long-range dependencies in 2D data and solve much more challenging tasks. It has close-to-optimal $\mathcal{O}(n^2 \log{n})$ complexity for processing $n \times n$ data matrix. Besides the common image classification and segmentation, we consider a diverse set of algorithmic tasks on matrices and graphs. Switchblade can infer highly complex matrix squaring and graph triangle finding algorithms purely from input-output examples. We show that our model is likewise suitable for logical reasoning tasks -- it attains perfect accuracy on Sudoku puzzle solving. Additionally, we introduce a new dataset for predicting the checkmating move in chess on which our model achieves 72.5% accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge