Unsupervised Training for Neural TSP Solver
Paper and Code
Jul 27, 2022
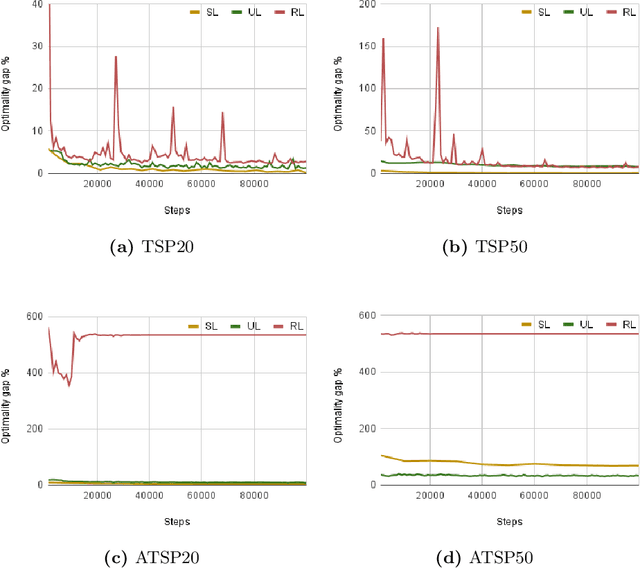
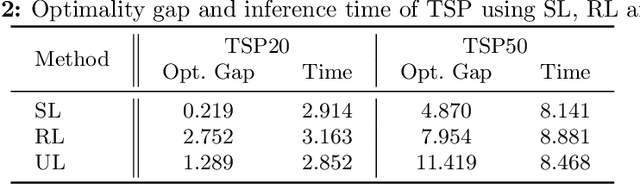

There has been a growing number of machine learning methods for approximately solving the travelling salesman problem. However, these methods often require solved instances for training or use complex reinforcement learning approaches that need a large amount of tuning. To avoid these problems, we introduce a novel unsupervised learning approach. We use a relaxation of an integer linear program for TSP to construct a loss function that does not require correct instance labels. With variable discretization, its minimum coincides with the optimal or near-optimal solution. Furthermore, this loss function is differentiable and thus can be used to train neural networks directly. We use our loss function with a Graph Neural Network and design controlled experiments on both Euclidean and asymmetric TSP. Our approach has the advantage over supervised learning of not requiring large labelled datasets. In addition, the performance of our approach surpasses reinforcement learning for asymmetric TSP and is comparable to reinforcement learning for Euclidean instances. Our approach is also more stable and easier to train than reinforcement learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge