Fast, accurate measurement of the worker populations of honey bee colonies using deep learning

Honey bees play a crucial role in pollination, contributing significantly to global agriculture and ecosystems. Accurately estimating hive populations is essential for understanding the effects of environmental factors on bee colonies, yet traditional methods of counting bees are time-consuming, labor-intensive, and prone to human error, particularly in large-scale studies. In this paper, we present a deep learning-based solution for automating bee population counting using CSRNet and introduce ASUBEE, the FIRST high-resolution dataset specifically designed for this task. Our method employs density map estimation to predict bee populations, effectively addressing challenges such as occlusion and overlapping bees that are common in hive monitoring. We demonstrate that CSRNet achieves superior performance in terms of time efficiency, with a computation time of just 1 second per image, while delivering accurate counts even in complex and densely populated hive scenarios. Our findings show that deep learning approaches like CSRNet can dramatically enhance the efficiency of hive population assessments, providing a valuable tool for researchers and beekeepers alike. This work marks a significant advancement in applying AI technologies to ecological research, offering scalable and precise monitoring solutions for honey bee populations.

Mitigating Estimation Errors by Twin TD-Regularized Actor and Critic for Deep Reinforcement Learning

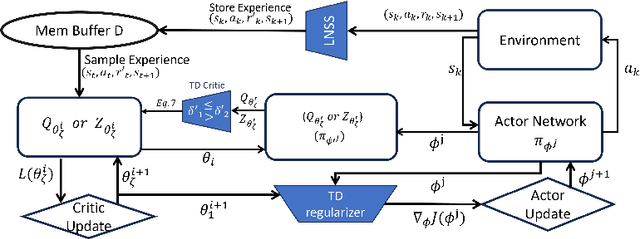
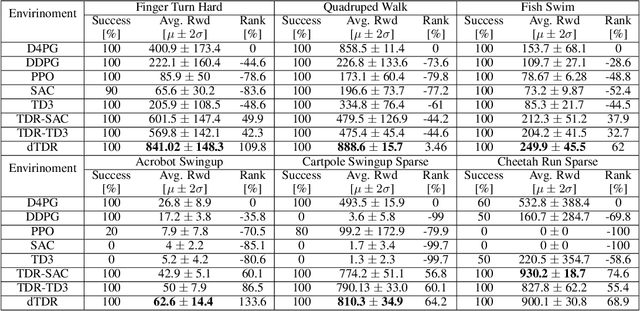
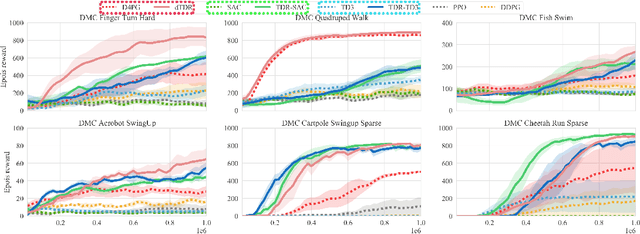
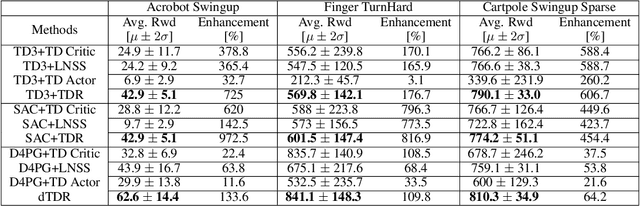
We address the issue of estimation bias in deep reinforcement learning (DRL) by introducing solution mechanisms that include a new, twin TD-regularized actor-critic (TDR) method. It aims at reducing both over and under-estimation errors. With TDR and by combining good DRL improvements, such as distributional learning and long N-step surrogate stage reward (LNSS) method, we show that our new TDR-based actor-critic learning has enabled DRL methods to outperform their respective baselines in challenging environments in DeepMind Control Suite. Furthermore, they elevate TD3 and SAC respectively to a level of performance comparable to that of D4PG (the current SOTA), and they also improve the performance of D4PG to a new SOTA level measured by mean reward, convergence speed, learning success rate, and learning variance.

Long N-step Surrogate Stage Reward to Reduce Variances of Deep Reinforcement Learning in Complex Problems

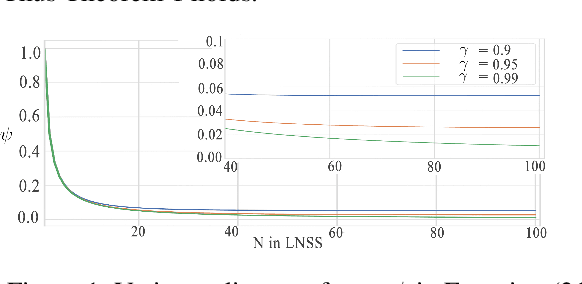
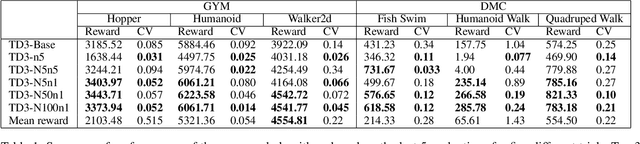
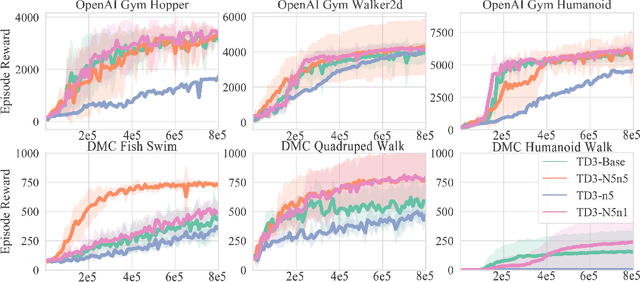
High variances in reinforcement learning have shown impeding successful convergence and hurting task performance. As reward signal plays an important role in learning behavior, multi-step methods have been considered to mitigate the problem, and are believed to be more effective than single step methods. However, there is a lack of comprehensive and systematic study on this important aspect to demonstrate the effectiveness of multi-step methods in solving highly complex continuous control problems. In this study, we introduce a new long $N$-step surrogate stage (LNSS) reward approach to effectively account for complex environment dynamics while previous methods are usually feasible for limited number of steps. The LNSS method is simple, low computational cost, and applicable to value based or policy gradient reinforcement learning. We systematically evaluate LNSS in OpenAI Gym and DeepMind Control Suite to address some complex benchmark environments that have been challenging to obtain good results by DRL in general. We demonstrate performance improvement in terms of total reward, convergence speed, and coefficient of variation (CV) by LNSS. We also provide analytical insights on how LNSS exponentially reduces the upper bound on the variances of Q value from a respective single step method