Long N-step Surrogate Stage Reward to Reduce Variances of Deep Reinforcement Learning in Complex Problems
Paper and Code
Oct 10, 2022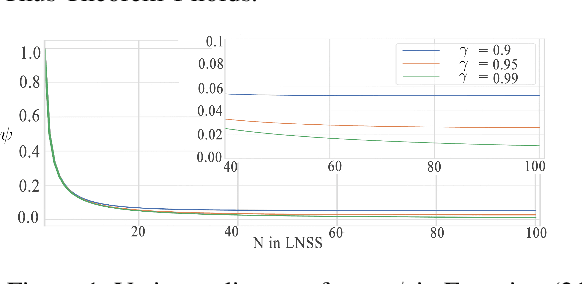
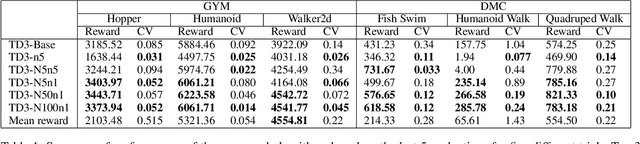
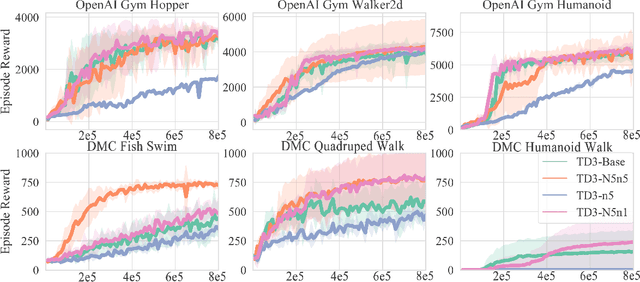

High variances in reinforcement learning have shown impeding successful convergence and hurting task performance. As reward signal plays an important role in learning behavior, multi-step methods have been considered to mitigate the problem, and are believed to be more effective than single step methods. However, there is a lack of comprehensive and systematic study on this important aspect to demonstrate the effectiveness of multi-step methods in solving highly complex continuous control problems. In this study, we introduce a new long $N$-step surrogate stage (LNSS) reward approach to effectively account for complex environment dynamics while previous methods are usually feasible for limited number of steps. The LNSS method is simple, low computational cost, and applicable to value based or policy gradient reinforcement learning. We systematically evaluate LNSS in OpenAI Gym and DeepMind Control Suite to address some complex benchmark environments that have been challenging to obtain good results by DRL in general. We demonstrate performance improvement in terms of total reward, convergence speed, and coefficient of variation (CV) by LNSS. We also provide analytical insights on how LNSS exponentially reduces the upper bound on the variances of Q value from a respective single step method
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge