Single-Image Super-Resolution Reconstruction based on the Differences of Neighboring Pixels

The deep learning technique was used to increase the performance of single image super-resolution (SISR). However, most existing CNN-based SISR approaches primarily focus on establishing deeper or larger networks to extract more significant high-level features. Usually, the pixel-level loss between the target high-resolution image and the estimated image is used, but the neighbor relations between pixels in the image are seldom used. On the other hand, according to observations, a pixel's neighbor relationship contains rich information about the spatial structure, local context, and structural knowledge. Based on this fact, in this paper, we utilize pixel's neighbor relationships in a different perspective, and we propose the differences of neighboring pixels to regularize the CNN by constructing a graph from the estimated image and the ground-truth image. The proposed method outperforms the state-of-the-art methods in terms of quantitative and qualitative evaluation of the benchmark datasets. Keywords: Super-resolution, Convolutional Neural Networks, Deep Learning

q-SNE: Visualizing Data using q-Gaussian Distributed Stochastic Neighbor Embedding

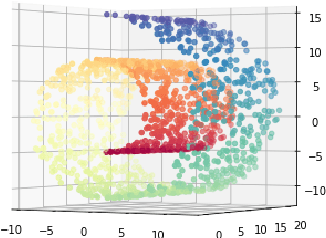
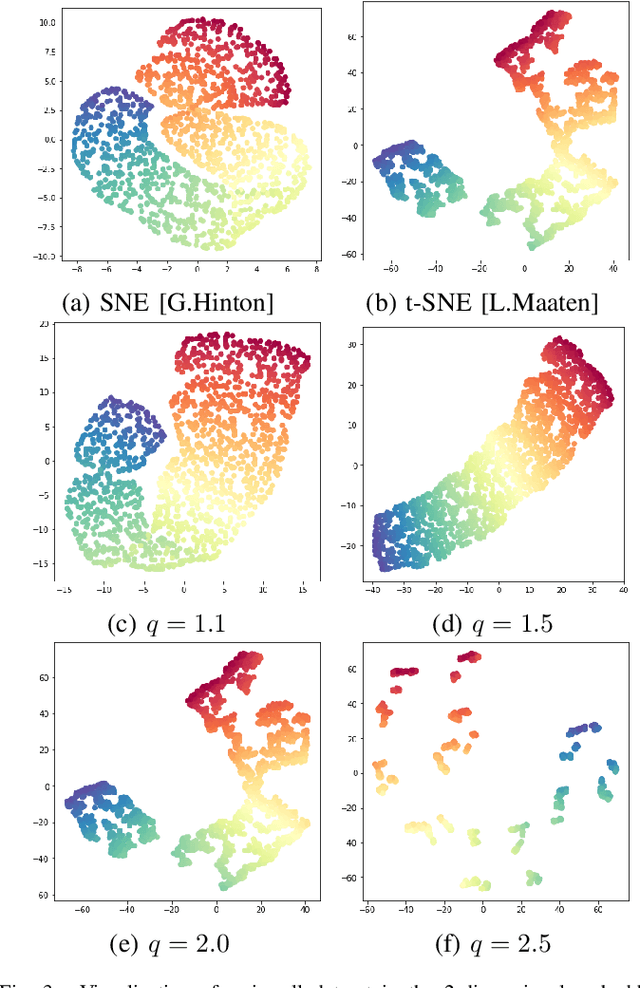
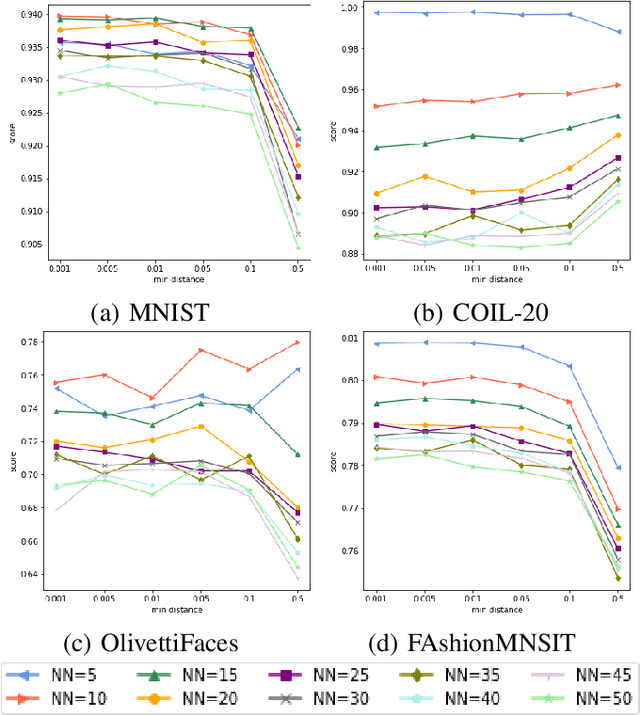
The dimensionality reduction has been widely introduced to use the high-dimensional data for regression, classification, feature analysis, and visualization. As the one technique of dimensionality reduction, a stochastic neighbor embedding (SNE) was introduced. The SNE leads powerful results to visualize high-dimensional data by considering the similarity between the local Gaussian distributions of high and low-dimensional space. To improve the SNE, a t-distributed stochastic neighbor embedding (t-SNE) was also introduced. To visualize high-dimensional data, the t-SNE leads to more powerful and flexible visualization on 2 or 3-dimensional mapping than the SNE by using a t-distribution as the distribution of low-dimensional data. Recently, Uniform manifold approximation and projection (UMAP) is proposed as a dimensionality reduction technique. We present a novel technique called a q-Gaussian distributed stochastic neighbor embedding (q-SNE). The q-SNE leads to more powerful and flexible visualization on 2 or 3-dimensional mapping than the t-SNE and the SNE by using a q-Gaussian distribution as the distribution of low-dimensional data. The q-Gaussian distribution includes the Gaussian distribution and the t-distribution as the special cases with q=1.0 and q=2.0. Therefore, the q-SNE can also express the t-SNE and the SNE by changing the parameter q, and this makes it possible to find the best visualization by choosing the parameter q. We show the performance of q-SNE as visualization on 2-dimensional mapping and classification by k-Nearest Neighbors (k-NN) classifier in embedded space compared with SNE, t-SNE, and UMAP by using the datasets MNIST, COIL-20, OlivettiFaces, FashionMNIST, and Glove.

Triplet Loss for Knowledge Distillation

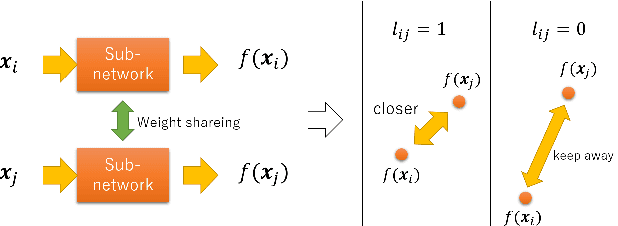
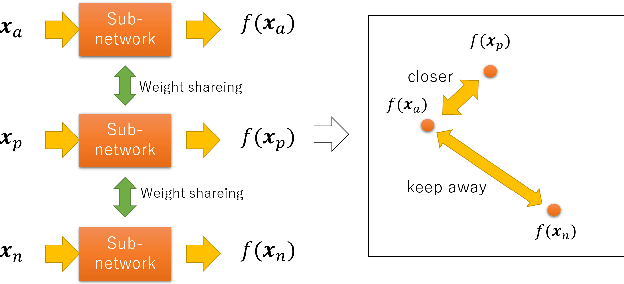
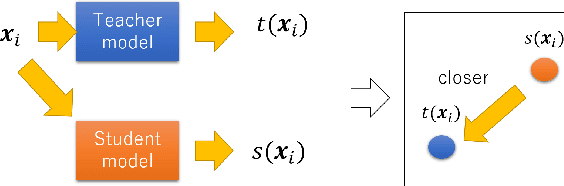
In recent years, deep learning has spread rapidly, and deeper, larger models have been proposed. However, the calculation cost becomes enormous as the size of the models becomes larger. Various techniques for compressing the size of the models have been proposed to improve performance while reducing computational costs. One of the methods to compress the size of the models is knowledge distillation (KD). Knowledge distillation is a technique for transferring knowledge of deep or ensemble models with many parameters (teacher model) to smaller shallow models (student model). Since the purpose of knowledge distillation is to increase the similarity between the teacher model and the student model, we propose to introduce the concept of metric learning into knowledge distillation to make the student model closer to the teacher model using pairs or triplets of the training samples. In metric learning, the researchers are developing the methods to build a model that can increase the similarity of outputs for similar samples. Metric learning aims at reducing the distance between similar and increasing the distance between dissimilar. The functionality of the metric learning to reduce the differences between similar outputs can be used for the knowledge distillation to reduce the differences between the outputs of the teacher model and the student model. Since the outputs of the teacher model for different objects are usually different, the student model needs to distinguish them. We think that metric learning can clarify the difference between the different outputs, and the performance of the student model could be improved. We have performed experiments to compare the proposed method with state-of-the-art knowledge distillation methods.

Adaptive Neuron-wise Discriminant Criterion and Adaptive Center Loss at Hidden Layer for Deep Convolutional Neural Network

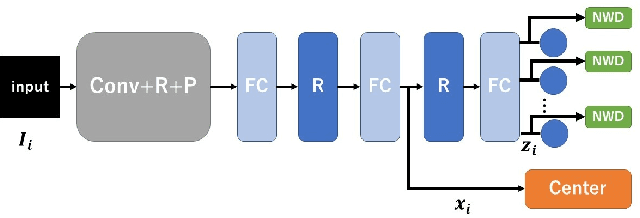
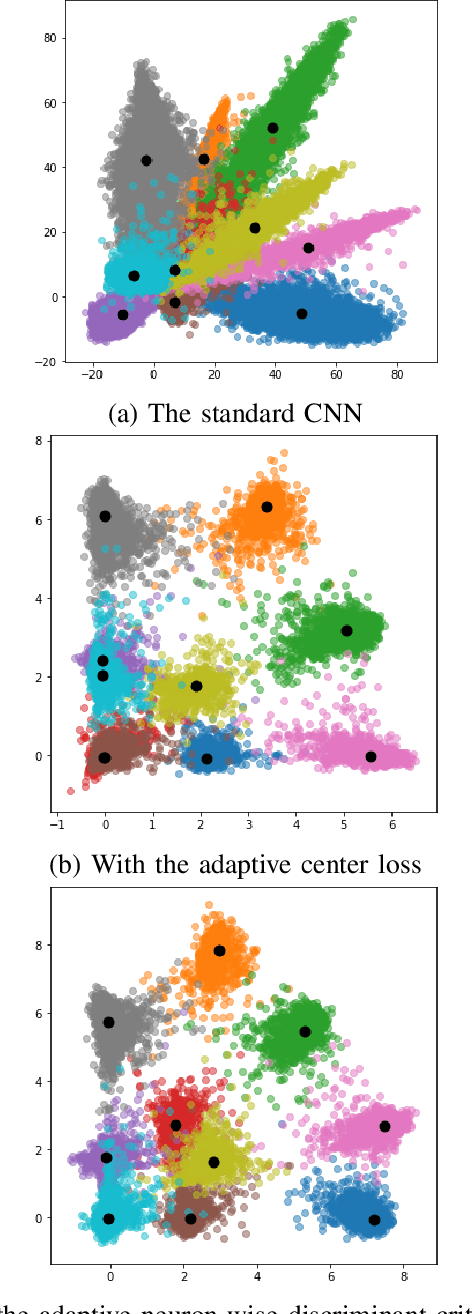
A deep convolutional neural network (CNN) has been widely used in image classification and gives better classification accuracy than the other techniques. The softmax cross-entropy loss function is often used for classification tasks. There are some works to introduce the additional terms in the objective function for training to make the features of the output layer more discriminative. The neuron-wise discriminant criterion makes the input feature of each neuron in the output layer discriminative by introducing the discriminant criterion to each of the features. Similarly, the center loss was introduced to the features before the softmax activation function for face recognition to make the deep features discriminative. The ReLU function is often used for the network as an active function in the hidden layers of the CNN. However, it is observed that the deep features trained by using the ReLU function are not discriminative enough and show elongated shapes. In this paper, we propose to use the neuron-wise discriminant criterion at the output layer and the center-loss at the hidden layer. Also, we introduce the online computation of the means of each class with the exponential forgetting. We named them adaptive neuron-wise discriminant criterion and adaptive center loss, respectively. The effectiveness of the integration of the adaptive neuron-wise discriminant criterion and the adaptive center loss is shown by the experiments with MNSIT, FashionMNIST, CIFAR10, CIFAR100, and STL10. Source code is at https://github.com/i13abe/Adaptive-discriminant-and-center

Hierarchical Group Sparse Regularization for Deep Convolutional Neural Networks

In a deep neural network (DNN), the number of the parameters is usually huge to get high learning performances. For that reason, it costs a lot of memory and substantial computational resources, and also causes overfitting. It is known that some parameters are redundant and can be removed from the network without decreasing performance. Many sparse regularization criteria have been proposed to solve this problem. In a convolutional neural network (CNN), group sparse regularizations are often used to remove unnecessary subsets of the weights, such as filters or channels. When we apply a group sparse regularization for the weights connected to a neuron as a group, each convolution filter is not treated as a target group in the regularization. In this paper, we introduce the concept of hierarchical grouping to solve this problem, and we propose several hierarchical group sparse regularization criteria for CNNs. Our proposed the hierarchical group sparse regularization can treat the weight for the input-neuron or the output-neuron as a group and convolutional filter as a group in the same group to prune the unnecessary subsets of weights. As a result, we can prune the weights more adequately depending on the structure of the network and the number of channels keeping high performance. In the experiment, we investigate the effectiveness of the proposed sparse regularizations through intensive comparison experiments on public datasets with several network architectures. Code is available on GitHub: "https://github.com/K-Mitsuno/hierarchical-group-sparse-regularization"