Multilinear analysis of quaternion arrays: theory and computation

Multidimensional quaternion arrays (often referred to as "quaternion tensors") and their decompositions have recently gained increasing attention in various fields such as color and polarimetric imaging or video processing. Despite this growing interest, the theoretical development of quaternion tensors remains limited. This paper introduces a novel multilinear framework for quaternion arrays, which extends the classical tensor analysis to multidimensional quaternion data in a rigorous manner. Specifically, we propose a new definition of quaternion tensors as $\mathbb{H}\mathbb{R}$-multilinear forms, addressing the challenges posed by the non-commutativity of quaternion multiplication. Within this framework, we establish the Tucker decomposition for quaternion tensors and develop a quaternion Canonical Polyadic Decomposition (Q-CPD). We thoroughly investigate the properties of the Q-CPD, including trivial ambiguities, complex equivalent models, and sufficient conditions for uniqueness. Additionally, we present two algorithms for computing the Q-CPD and demonstrate their effectiveness through numerical experiments. Our results provide a solid theoretical foundation for further research on quaternion tensor decompositions and offer new computational tools for practitioners working with quaternion multiway data.

Polarimetric phase retrieval: uniqueness and algorithms

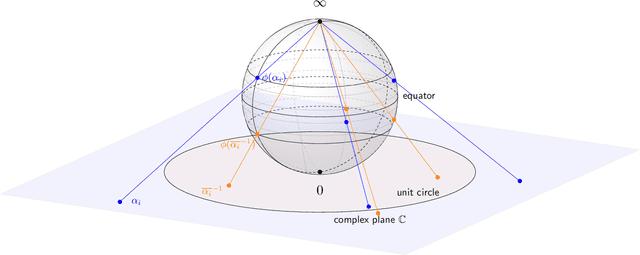
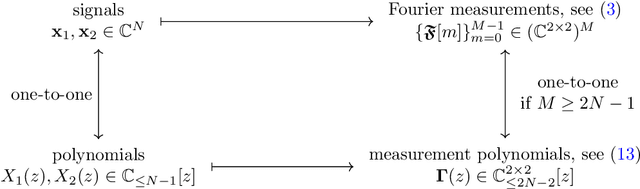
This work introduces a novel Fourier phase retrieval model, called polarimetric phase retrieval that enables a systematic use of polarization information in Fourier phase retrieval problems. We provide a complete characterization of uniqueness properties of this new model by unraveling equivalencies with a peculiar polynomial factorization problem. We introduce two different but complementary categories of reconstruction methods. The first one is algebraic and relies on the use of approximate greatest common divisor computations using Sylvester matrices. The second one carefully adapts existing algorithms for Fourier phase retrieval, namely semidefinite positive relaxation and Wirtinger-Flow, to solve the polarimetric phase retrieval problem. Finally, a set of numerical experiments permits a detailed assessment of the numerical behavior and relative performances of each proposed reconstruction strategy. We further highlight a reconstruction strategy that combines both approaches for scalable, computationally efficient and asymptotically MSE optimal performance.

A general framework for constrained convex quaternion optimization

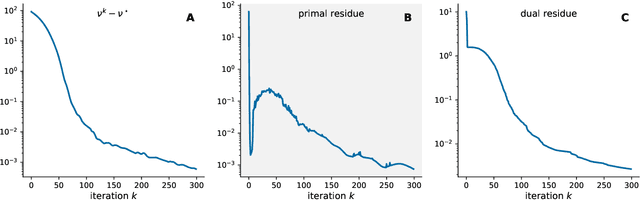
This paper introduces a general framework for solving constrained convex quaternion optimization problems in the quaternion domain. To soundly derive these new results, the proposed approach leverages the recently developed generalized $\mathbb{HR}$-calculus together with the equivalence between the original quaternion optimization problem and its augmented real-domain counterpart. This new framework simultaneously provides rigorous theoretical foundations as well as elegant, compact quaternion-domain formulations for optimization problems in quaternion variables. Our contributions are threefold: (i) we introduce the general form for convex constrained optimization problems in quaternion variables, (ii) we extend fundamental notions of convex optimization to the quaternion case, namely Lagrangian duality and optimality conditions, (iii) we develop the quaternion alternating direction method of multipliers (Q-ADMM) as a general purpose quaternion optimization algorithm. The relevance of the proposed methodology is demonstrated by solving two typical examples of constrained convex quaternion optimization problems arising in signal processing. Our results open new avenues in the design, analysis and efficient implementation of quaternion-domain optimization procedures.