A general framework for constrained convex quaternion optimization
Paper and Code
Feb 04, 2021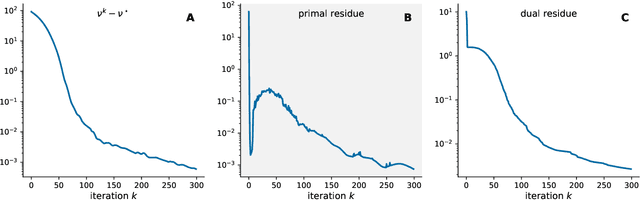
This paper introduces a general framework for solving constrained convex quaternion optimization problems in the quaternion domain. To soundly derive these new results, the proposed approach leverages the recently developed generalized $\mathbb{HR}$-calculus together with the equivalence between the original quaternion optimization problem and its augmented real-domain counterpart. This new framework simultaneously provides rigorous theoretical foundations as well as elegant, compact quaternion-domain formulations for optimization problems in quaternion variables. Our contributions are threefold: (i) we introduce the general form for convex constrained optimization problems in quaternion variables, (ii) we extend fundamental notions of convex optimization to the quaternion case, namely Lagrangian duality and optimality conditions, (iii) we develop the quaternion alternating direction method of multipliers (Q-ADMM) as a general purpose quaternion optimization algorithm. The relevance of the proposed methodology is demonstrated by solving two typical examples of constrained convex quaternion optimization problems arising in signal processing. Our results open new avenues in the design, analysis and efficient implementation of quaternion-domain optimization procedures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge