Multilinear analysis of quaternion arrays: theory and computation

Multidimensional quaternion arrays (often referred to as "quaternion tensors") and their decompositions have recently gained increasing attention in various fields such as color and polarimetric imaging or video processing. Despite this growing interest, the theoretical development of quaternion tensors remains limited. This paper introduces a novel multilinear framework for quaternion arrays, which extends the classical tensor analysis to multidimensional quaternion data in a rigorous manner. Specifically, we propose a new definition of quaternion tensors as $\mathbb{H}\mathbb{R}$-multilinear forms, addressing the challenges posed by the non-commutativity of quaternion multiplication. Within this framework, we establish the Tucker decomposition for quaternion tensors and develop a quaternion Canonical Polyadic Decomposition (Q-CPD). We thoroughly investigate the properties of the Q-CPD, including trivial ambiguities, complex equivalent models, and sufficient conditions for uniqueness. Additionally, we present two algorithms for computing the Q-CPD and demonstrate their effectiveness through numerical experiments. Our results provide a solid theoretical foundation for further research on quaternion tensor decompositions and offer new computational tools for practitioners working with quaternion multiway data.

Tensor-based framework for training flexible neural networks

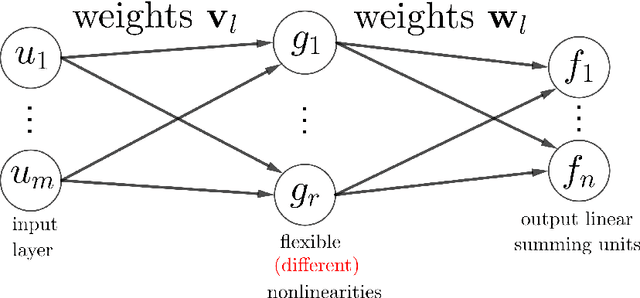
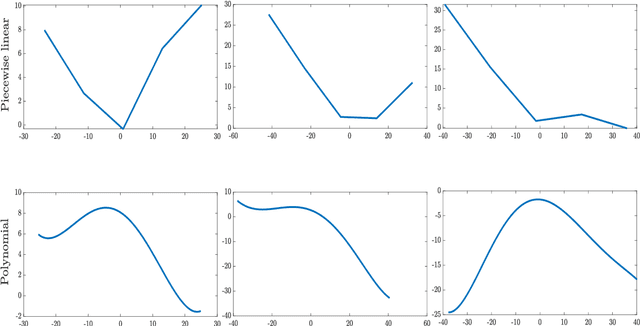
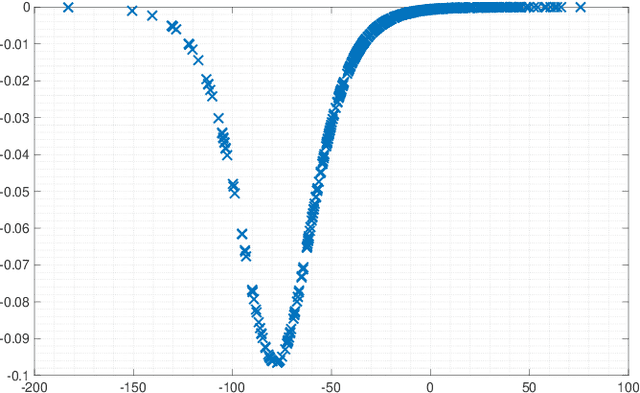
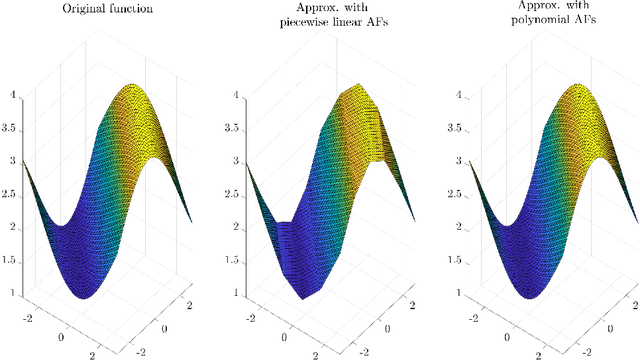
Activation functions (AFs) are an important part of the design of neural networks (NNs), and their choice plays a predominant role in the performance of a NN. In this work, we are particularly interested in the estimation of flexible activation functions using tensor-based solutions, where the AFs are expressed as a weighted sum of predefined basis functions. To do so, we propose a new learning algorithm which solves a constrained coupled matrix-tensor factorization (CMTF) problem. This technique fuses the first and zeroth order information of the NN, where the first-order information is contained in a Jacobian tensor, following a constrained canonical polyadic decomposition (CPD). The proposed algorithm can handle different decomposition bases. The goal of this method is to compress large pretrained NN models, by replacing subnetworks, {\em i.e.,} one or multiple layers of the original network, by a new flexible layer. The approach is applied to a pretrained convolutional neural network (CNN) used for character classification.